A river is flowing from west to east at α speed of 5 metre per minute. A man on the south bank of the river, capable of swimming at 10 metre per minute in still water, wants to swim across the river by the shortest path . Calculate the direction in which he should swim.
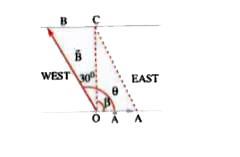
The situation is shown in fig.
OA=A, represents velocity of river which is 5mmt−1
OB=B , represents velocity of man in still water which is 10mmt−1
The man starts swimming from O and goes along OB to reach C by shortest possible path .
Here ,∠AOC=β=90∘
Here, A=5mmt−1,B=10mmt−1β=90∘,θ=?
From formula , tanβ=BsinθA+Bcosθ
putting values, we get ,tan90∘=10sinθ5+10cosθ=∞(∈f∈ite)
Hence, 5+10cosθ=0or10cosθ=−5
(or) cosθ=−0.5=cos120∘i.e.,θ=120∘
It makes ∠COB=30∘
The man should swim along OB which is 30∘ west of north .
Topper's Solved these Questions
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - Short Answer type question
4 Videos
- ELEMENTS OF VECTORS BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORS EXERCISE - Very Short Answer type Questions
8 Videos
- ELASTICITYBOOK - AAKASH SERIESCHAPTER - ELASTICITYEXERCISE - Questions for Descriptive Answers
10 Videos
- EXPANSION OF GASESBOOK - AAKASH SERIESCHAPTER - EXPANSION OF GASESEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS
4 Videos
Similar Questions
A river is flowing from west to east at a speed of 5 metres per minute.A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
View SolutionA river is flowing from west to east at a speed of 5 metres per minute.A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
View Solution
Knowledge Check
A river is flowing from west to east at a speed of 5 metres per minute.A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
ADue northB30∘ each of northC30∘ west of northD60∘ east of northA river is flowing from west to east at a speed of 5metresperminute . A man on the south bank of the river , capable of swimming at 10metresperminute, in still water , wants to swim across the river in the shortest time . He should swim in a direction
ADue northB30∘ each of northC30∘ west of northD60∘ east of northA river is flowing from west to east at a speed of 5 metres per minute.A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
Adue northB30∘ east of northC30∘ west of northD60∘ east of north
A river is flowing from west to east at a speed of 5metresperminute . A man on the south bank of the river , capable of swimming at 10metresperminute, in still water , wants to swim across the river in the shortest time . He should swim in a direction
View SolutionA river is following from west to east at a speed of 5m/minute. A boy on the south bank of the river, capable of swimming at 10 meters/minute in still water, wants to swin across the river in the shortest time, (i) Find the direction in which he should swin, (ii) find the direction when drift along the river is zero.
View SolutionA river is following from west to east at a speed of 5m/minute. A boy on the south bank of the river, capable of swimming at 10 meters/minute in still water, wants to swin across the river in the shortest time, (i) Find the direaction in which he should swin, (ii) find the direction when drift along the river is zero.
View SolutionA river is flowing from west to east at a speed of 5m/s. A man on the south bank of the river capable of swimming at 10m/s in a still water wants to swim, across the river in a shortest time. He should swim in a direction
View SolutionA river is flowing from east to west at a speed of 5m/min. A man on south bank of river, capable of swimming 10m/min in still water, wants to swim across the river in shortest time. He should swim
View Solution
