Name the laws associated with the following equation. ∮→E.→dt=m0(IC+ε0dϕEdt
∮→E.→dt = 0. This equation is based on the fact that magnetic monopoles do not exist.
Topper's Solved these Questions
Similar Questions
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
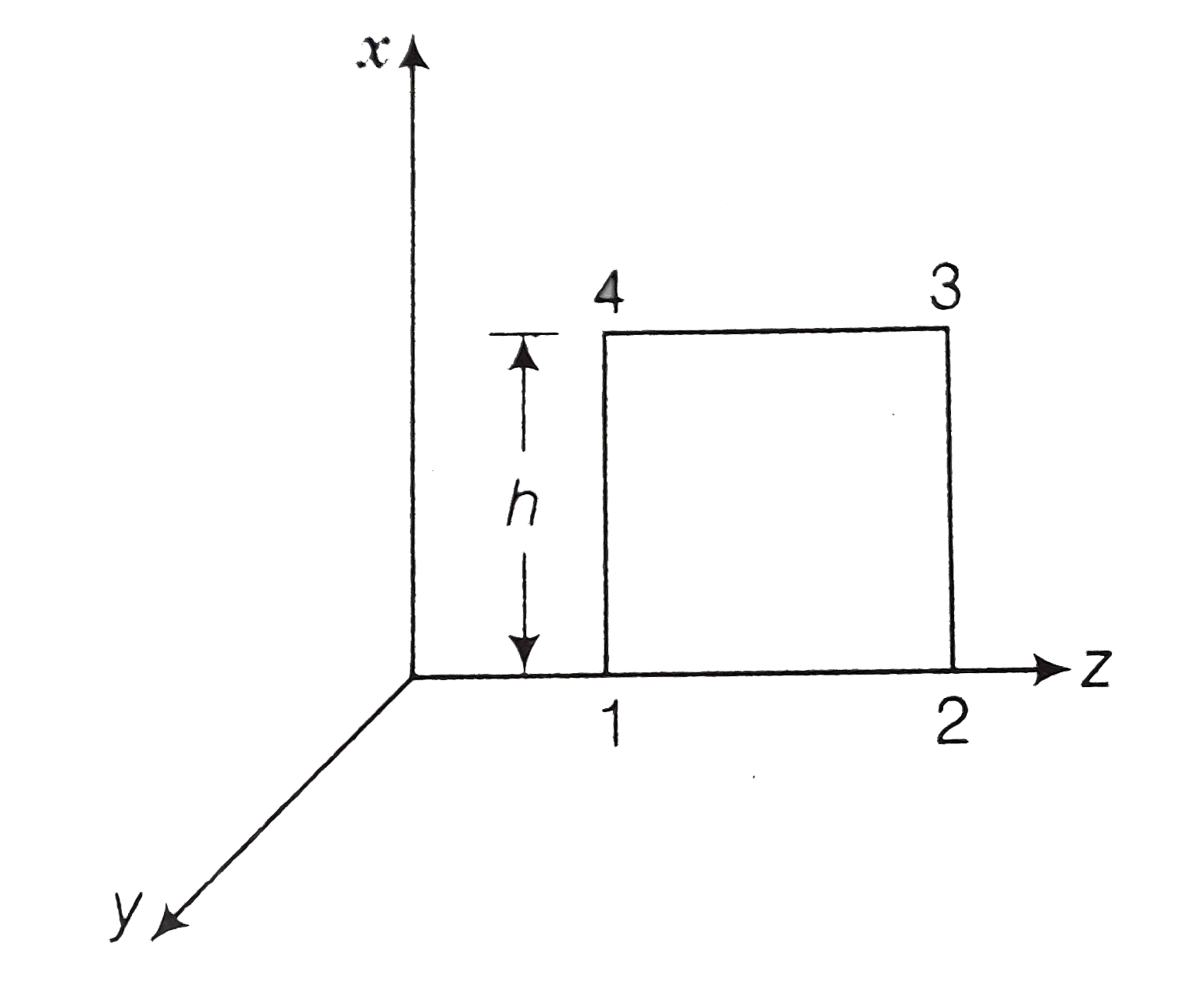
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0
View SolutionA plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0

View Solution
Knowledge Check
The maxwell’s equation :
∮→B.→dl=μ0(i+ɛ0.dϕEdt) is a statement of -AFaraday’s law of inductionBModified Ampere’s lawCGauss’s law of electricityDGauss’s law of magnetismDimensions of ε0dϕEdt are same as that of
A[AT]B[A]C[ML2T−2]D[ML−1T−2]In each question, there .is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Eac!h question bas 4 options (a), (b), (c) and (d), ONLY ONE of these four options is correct.
In the given table, Column I shows different laws in electromagnetic theory, Column II shows the related physica l quantities and Column III shows the equations related to the different laws.
Column IColumn IIColumn II(I) Gauss's law (i) Magnetism (J)∮→B.d→s=μ0ε0dϕEdt+μ0dqdt(II)Ampere's law(ii)Current (K) ∮→B.d→A=0(III)Gauss's law (iii)Induction (L)∮→E.d→s=dϕBdt(IV)Faraday's (iv)Electricity(M)∮→E.d→A=qε
Jn which law there are no magnetic monopoles invo lved?A(1) (ii) (J)B(III) (i) (K)C(II) (iii) (L)D(I) (i) (M)
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0

View SolutionWrite Maxwell’s generalization of Ampere’s Circuital Law. Show that in the process the current produced within the plates of the capacitor is
i=ε0dΦEdt
where ΦE is the electric. flux produced during charging of the capacitor plates.
View SolutionIn each question, there .is a table having 3 columns and 4 rows. Based on the table, there are 3 questions. Eac!h question bas 4 options (a), (b), (c) and (d), ONLY ONE of these four options is correct.
In the given table, Column I shows different laws in electromagnetic theory, Column II shows the related physica l quantities and Column III shows the equations related to the different laws.
Column IColumn IIColumn II(I) Gauss's law(i)Magnetism (J)∮→B.d→s=μ0ε0dϕEdt+μ0dqdt(II)Ampere's law(ii)Current (K) ∮→B.d→A=0(III)Gauss's law (iii)Induction (L)∮→E.d→s=dϕBdt(IV)Faraday's (iv)Electricity (M)∮→E.d→A=qε
In which law does the charge create diverging electric fields?
View SolutionMatch the statements in Column I labeled as (a), (b), (c), and (d) with those in Column II labeled as (p), (q), (r), and (s).Any given statement in Column I can have correct matching with one or more statements in Column II.
Column IColumn II(a)∮→E.d→s=−dϕBdt(p)Maxwell's law of induction(b)∮→B.d→s=μ0ε0dϕEdt(q)Ampere-Maxwell law(c)∮→B.d→s=μ0Ienc(r)Ampere's law(d)∮→B.d→l=u0ε0dϕEdt+μ0Ienc(s)Faraday's law of indcution
View SolutionThe maxwells four equations are written as
(i) ∮→E.−→dS=q0ε0
(ii) ∮→B.−→dS=0
(iii) ∮→E.→dl=ddt∮→B.−→dS
(iv) ∮→B.→dl=μ0ε0ddt∮→E.−→dS
The equations which have sources of →E and →B are
View Solution
