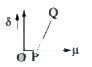
Angle of deviation (delta) for a prism (refractive index μ and supposing prism angle A to be small) is given by:
(δ)=(μ−1μ+1)A
(δ)=(μ−1)A
(δ)=sin(A+δ)2Sin(A2)
(δ)=(μ+1)A
The correct Answer is:B
Topper's Solved these Questions
Similar Questions
Angle of minimum deviation for a prism of refractive index 1.5 is equal to the angle of prism of given prism. Then, the angle is prism is….
(sin48∘36'=0.75)
View SolutionFor a small angled prism, angle of minimum deviation (δ) varies with the refractive index of the prism as shown in the graph
View Solution
Knowledge Check
Angle of deviation (δ) by a prism (refractive index = μ and supposing the angle of prism A to be small) can be given by
Aδ=(μ−1)ABδ=(μ+1)ACδ=sin(A+δ)2sin(A)2Dδ=μ−1μ+1AAngle of minimum deviation for a prism of refractive index 1.5 is equal to the angle of prism of given prism. Then, the angle is prism is….
(sin48∘36'=0.75)A80∘B41∘24'C60∘D82∘48'The angle of minimum deviation of a prism of refractive index √3 is equal to its refracting angle. Then the refracting angle of that prism is
A30∘B45∘C60∘D90∘
If δmin is the minimum deviation through a prism and μ is refractive index and A is angle of prism
View SolutionThe minimum deviation on a prism of refractive index √3 is equal to the angle of prism. Find the angle of the prism.
View SolutionThe light ray is incidence at angle of 60∘ on a prism of angle 45∘ . When the light ray falls on the other surface at 90∘ , the refractive index of the material of prismμ and the angle of deviation δ are given by
View SolutionThe angle of minimum deviation of a prism of refractive index √3 is equal to its refracting angle. Then the refracting angle of the prism is
View SolutionFor a small angled prism, angle of prism A of minimum deviation(δ) varies with the refractive index of the prism as shown in the graph

View Solution
