Question

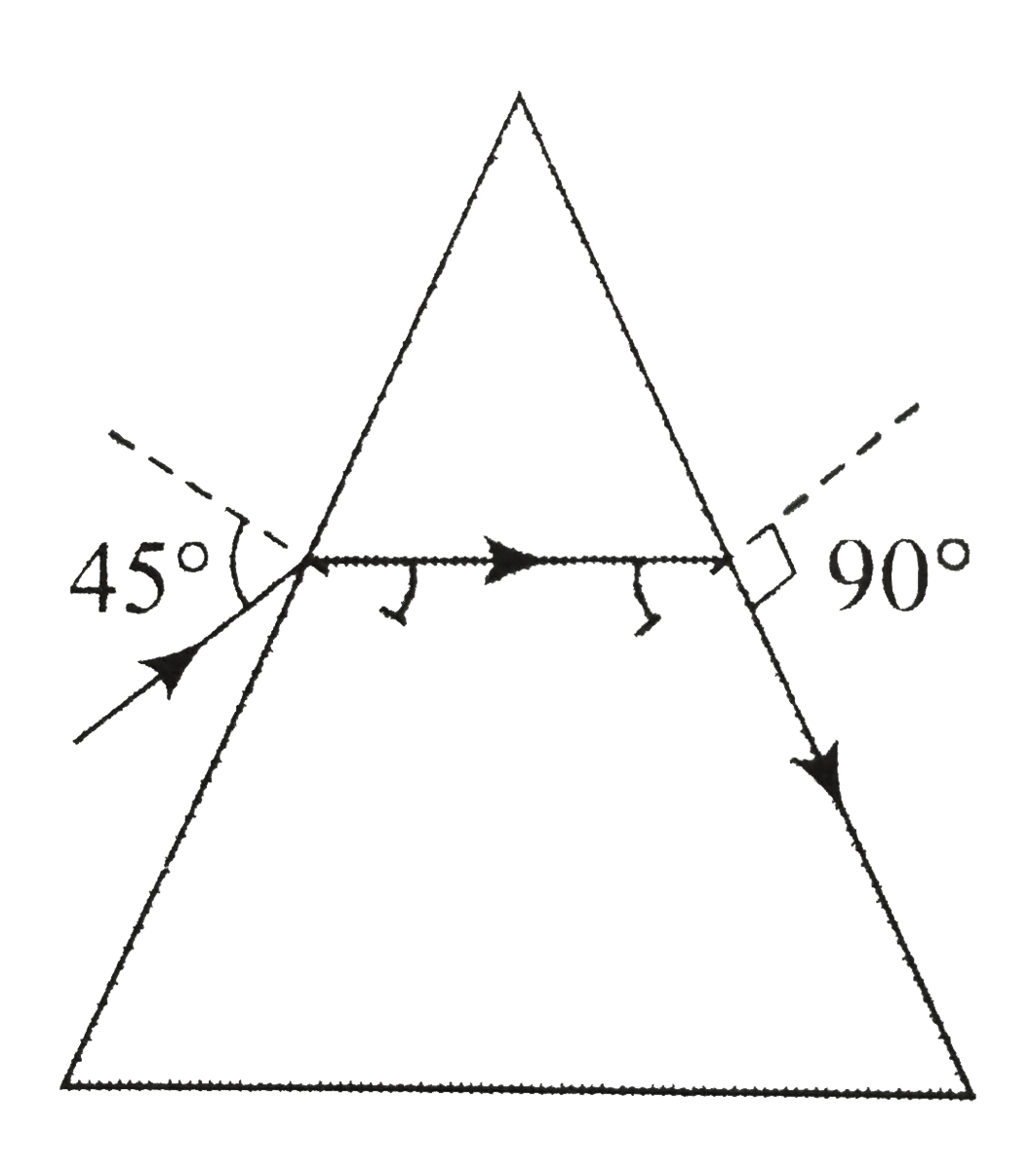
The light ray is incidence at angle of ${60}^{\circ }$ on a prism of angle ${45}^{\circ }$ . When the light ray falls on the other surface at ${90}^{\circ }$ , the refractive index of the material of prism$\mu$ and the angle of deviation $\delta$ are given by

Options

A. `mu=sqrt(2), delta=30^(@)`
B. `mu=1.5, delta=15^(@)`
C. `mu=(sqrt(3))/(2), delta=30^(@)`
D. `mu=sqrt((3)/(2)), delta=15^(@)`

Answer

D

Explanation

To solve the problem step by step, we will determine the refractive index (μ) of the prism and the angle of deviation (δ) based on the given information.

Step 1: Identify the angles
- The angle of incidence (I) is given as \(60^\circ\).
- The angle of the prism (A) is given as \(45^\circ\).
- The angle of refraction at the second surface (r2) is \(90^\circ\).

Step 2: Use the property of the prism
According to the property of a prism, the sum of the angles of refraction at the two surfaces is equal to the angle of the prism:
\( r_1 + r_2 = A \)
Given that \(r_2 = 0^\circ\) (because the ray exits at \(90^\circ\)), we can write:
\( r_1 + 0 = 45^\circ \implies r_1 = 45^\circ \)

Step 3: Apply Snell's Law at the first surface
Using Snell's Law at the first surface, we have:
\( \mu_1 \sin I = \mu_2 \sin r_1 \)
Where:
- \(\mu_1 = 1\) (for air)
- \(I = 60^\circ\)
- \(r_1 = 45^\circ\)
- \(\mu_2 = \mu\) (refractive index of the prism)

Substituting the values, we get:
\( 1 \cdot \sin(60^\circ) = \mu \cdot \sin(45^\circ) \)

Step 4: Solve for the refractive index (μ)
We know:
- \(\sin(60^\circ) = \frac{\sqrt{3}}{2}\)
- \(\sin(45^\circ) = \frac{1}{\sqrt{2}}\)

Substituting these values into the equation:
\( \frac{\sqrt{3}}{2} = \mu \cdot \frac{1}{\sqrt{2}} \)

Rearranging gives:
\( \mu = \frac{\frac{\sqrt{3}}{2}}{\frac{1}{\sqrt{2}}} = \frac{\sqrt{3}}{2} \cdot \sqrt{2} = \frac{\sqrt{6}}{2} \)

Step 5: Calculate the angle of deviation (δ)
The angle of deviation (δ) can be calculated using the formula:
\( \delta = (\mu - 1) \cdot A \)
Substituting the values:
\( \delta = \left(\frac{\sqrt{6}}{2} - 1\right) \cdot 45^\circ \)

Step 6: Simplify the expression
Calculating \(\frac{\sqrt{6}}{2} - 1\):
\( \delta = \left(\frac{\sqrt{6} - 2}{2}\right) \cdot 45^\circ \)

Step 7: Final calculation
Now, we can compute the numerical value of δ:
\( \delta = \frac{\sqrt{6} - 2}{2} \cdot 45^\circ \)

Conclusion
Thus, the refractive index of the prism is:
\( \mu = \frac{\sqrt{6}}{2} \)
And the angle of deviation is:
\( \delta = 15^\circ \)