For a photosensitive surface , work function is 3.3×10−19 J. Taking plank's constant to be 6.6×10−34 Js. Find threshold frequency.
Here W0=3.3×10−19J
h=6.6×10−34Js
Threshold frequency v0=W0h=3.3×10−196.6×10−34=5×1014Hz
Topper's Solved these Questions
Similar Questions
Knowledge Check
The work function of a photoelectric metal is 3.31 eV. If h=6.62×10−34Js, then its threshold frequency will be
A8×1014 HzB8×1010HzC5×1015 HzD3×1014 HzThe de - Broglie wavelength of an electron having 80ev of energy is nearly
(1eV=1.6×10−19J, Mass of electron =9×10−31kg Plank's constant =6.6×10−34J−sec)A140ÅB0.14ÅC14ÅD1.4ÅAn electron beam has a kinetic energy equal to 100 eV . Find its wavelength associated with a beam , if mass of electron =9.1×10−31 kg and 1 eV =1.6×10−19J . (Planks's constant = 6.6×10−34J−s)
A24.6ÅB0.12ÅC1.2ÅD6.3Å
A metal whose work function is 3.3eV is illuminated by light of wavelength 3×10−7m. What is the threshold frequency for photoelectric emission? Plank's constant =6.6×10−34 Js?
View SolutionFind the maximum velocity of photoelectrons emitted by radiation of frequency 3×1015 Hz from a photoelectric surface having a work function of 4.0 eV. Given h=6.6×10−34 Js and 1 eV = 1.6×10−19 J.
View SolutionFind the maximum velocity of photoelectrons emitted by radiation of frequency 3×1015 Hz from a photoelectric surface having a work function of 4.0 eV. Given h=6.6×10−34 Js and 1 eV = 1.6×10−19 J.
View Solution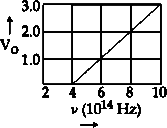
the stopping potential Vo (in volt) as a function of frequency (v) for a soidum emitter, is shown in the figure. The work function of sodium from the data plotted in the figure. Will be:
[ given plank's constant (h)=6.63×10−34Js, electron charge e=1.6×10−19C)
View SolutionAn electron beam has a kinetic energy equal to 100 eV . Find its wavelength associated with a beam , if mass of electron =9.1×10−31 kg and 1 eV =1.6×10−19J . (Planks's constant = 6.6×10−34J−s)
View Solution
