The expression 1λ=R(1p2−1n2) after the Balmer's work is known as R=(me48h3c(ε0)2)
Balmer's formula
Bohr's formula
Paschen's formula
Lyman's formula
The correct Answer is:A
Topper's Solved these Questions
Similar Questions
Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion. the wavelength of first line of balmer region.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Calculate the iongest wavelength in A(1Å=10−10m) in the 'Balmer series of singly ionized helium (He+) Ignore nuclear motion in your calculation.
View Solution
Knowledge Check
For the Paschen series the values of n1 and n2 in the expression ΔE=RH.c(1n21−1n22)
An1=1,n2=2,3,4 …Bn1=2,n2=3,4,5Cn13,n2=4,5,6 …….Dn1=4,n2=5,6,7 ……
Hydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Calculate the iongest wavelength in A(1Å=10−10m) in the 'Balmer series of singly ionized helium (He+) Ignore nuclear motion in your calculation.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the loest energy and the radius of the Bohr orbit of the muonic hydrogen atom. Ignore the motion of the nucleus in your calculation. The radius of the Bohr orbit of a hydrogen atom
(called the Bohr radius,a0=ε0h2mee2∏is0.53Å)
The classical picture of an ''orbit'' in Bohr's theory has now been replaced by the quantum mechanical nation of an 'orbital'. The orbital ψ1σ1s(r) for the ground state of a hydrogen atom is given by
ψ1s(r)=1√∏a30era0
where r is the distance of the electron from the nucleus and a0 is the Bohr radius.
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
Determine the values of the dissociation energies (DeineV) of the H2 molecule corresponding to channel (i)
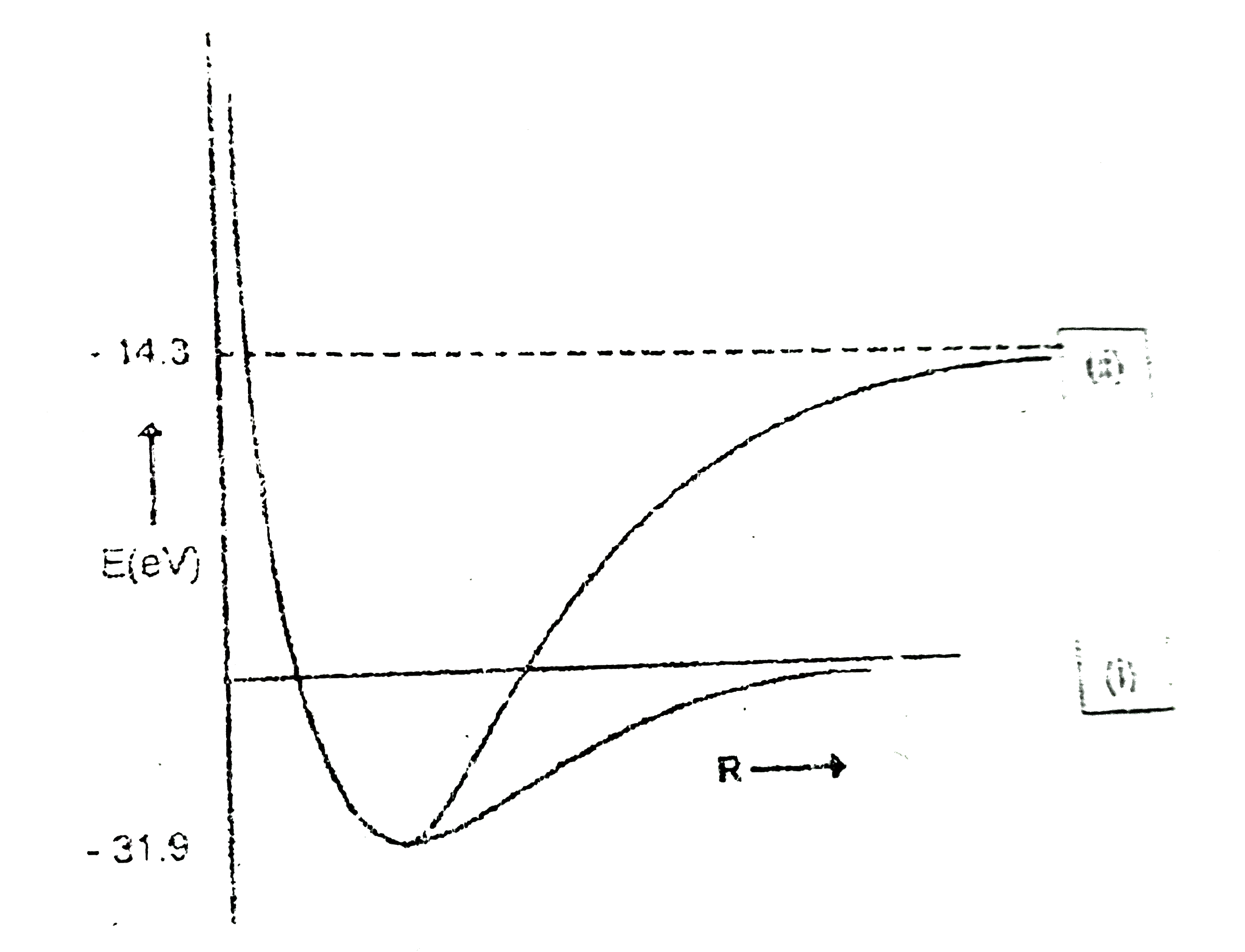
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
From the given data, calculate the energy change for the process
H−→H+e−
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
From the given data, calculate the energy change for the process
H−→H+e−
View SolutionHydrogen Atom and Hydrogen Molecule
The observed wavelengths in the line spectrum of hydrogen atom were first expressed in terms of a series by johann Jakob Balmer, a Swiss teacher. Balmer's empirical empirical formula is
1λ=RH(122−1n2), N=3,4,5
RH=Mee48ε20h3c=109.678cm−1
Here,
RH is the Rydberg Constant, me is the mass of electron. Niels Bohr derived this expression theoretically in 1913. The formula is easily generalized to any one electron atom//ion.
H− is a two-electron atomic system. Assuming that the Bohr energy formula is valid for each electron with nuclear charge Z replaced by Zeff' calculate Zeff for H−.
View SolutionA parallel combination of two cells of emfs ε1 and ε2, and internal resistance r1 and r2 is used to supply current to a load of resistance R. Write the expression for the current through the load in terms of ε1,ε2,r1 and r2.
View Solution
