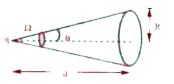
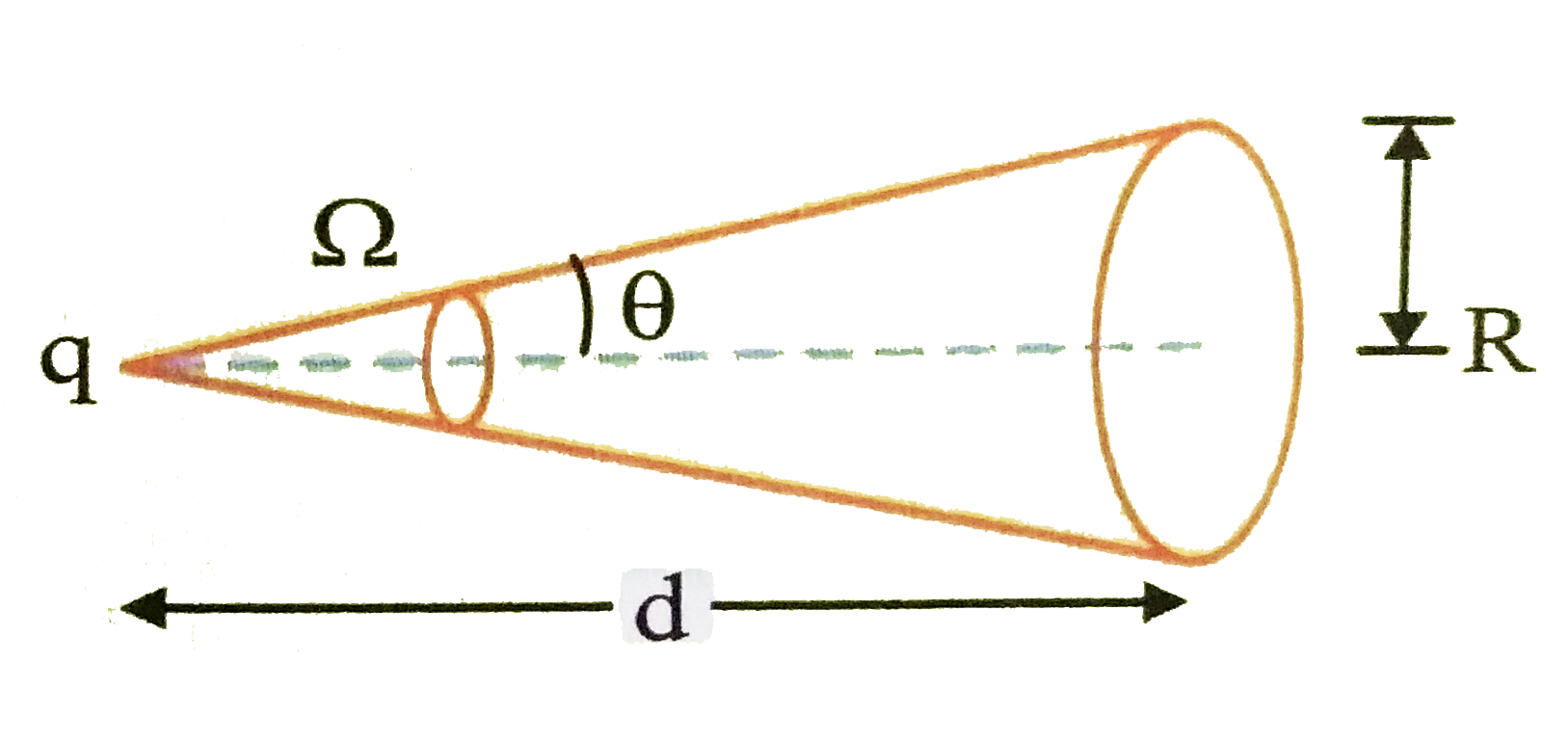
A point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge.

Text Solution

Verified by Experts

We know that total flux originated from a point charge q in all directions is $\frac{q}{\in_{0}}$ .
This flux is originated in a solid angle $4 π$ . In the given case solid angle subtended by the cone subtended by the disc at the point charge is $ω = 2 π (1 - cos θ)$
So, the flux of q which is passing through the surface of the disc is
$ϕ = \frac{q}{\in_{0}} \frac{ω}{4 π} = \frac{q}{2 \in_{0}} (1 - cos θ)$
From the figure , $cos θ = \frac{d}{\sqrt{d^{2} + R^{2}}}$
so, $ϕ = \frac{q}{2 \in_{0}} {1 - \frac{d}{\sqrt{d^{2} + R^{2}}}}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Similar Questions

Knowledge Check

Question 1 - Select One
A point charge $q$ is placed at a distance $a / 2$ directly above the center of a square of side $a$ . The electric flux through the square is
A $\frac{q}{ε_{0}}$
B $\frac{q}{π ε_{0}}$
C $\frac{q}{4 ε_{0}}$
D $\frac{q}{6 ε_{0}}$
Question 2 - Select One
A position charge Q is placed at a distance of 4R above the centre of a disc of radius R. The magnitude of flux through the disc is $ϕ$ . Now a hemispherical shell of radius R is placed over the disc such that it forms a closed surface. The flux through the curved surface (taking direction of area vector along outward normal as positive), is -

Azero
B $ϕ$
C $- ϕ$
D $2 ϕ$
Question 3 - Select One
a point charge $q$ is placed at the centre of a cylinder of length $L$ and radius $R$ the electric flux through the curved surface of the cylinder is
A $\frac{q}{ε_{0}} \frac{L}{\sqrt{L^{2} + R^{2}}}$
B $\frac{q}{ε_{0}} \frac{L}{\sqrt{L^{2} + 2 R^{2}}}$
C $\frac{q}{ε_{0}} \frac{L}{\sqrt{L^{2} + 4 R^{2}}}$
D $\frac{q}{2 ε_{0}}$

Recommended Questions

Home
Ask Doubt
Profile