A point charge q is placed at a distance a/2 directly above the centre of a square of side a. The electric flux through the square is
(a) q/ε0
(b) q/2ε0
(c) q4ε0
(d) q/ε0
The correct Answer is:D
To solve the problem of finding the electric flux through a square when a point charge q is placed above it, we can follow these steps:
Step 1: Understand the Geometry
We have a square of side a and a point charge q located at a distance a2 directly above the center of the square.
Step 2: Visualize the Cube
The square can be thought of as one face of a cube. The cube has six faces, and the charge q is located at the center of the cube, above the square face.
Step 3: Use Gauss's Law
According to Gauss's law, the total electric flux Φ through a closed surface is given by:
Φ=qencϵ0
where qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
Step 4: Calculate Total Flux Through the Cube
Since the charge q is at the center of the cube, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
Step 5: Calculate Flux Through One Face of the Cube
Since the cube has six faces and the charge is symmetrically placed, the flux will be evenly distributed among the six faces. Therefore, the flux through one face (which is our square) is:
Φsquare=Φtotal6=q6ϵ0
Conclusion
Thus, the electric flux through the square is:
Φ=q6ϵ0
We have a square of side a and a point charge q located at a distance a2 directly above the center of the square.
The square can be thought of as one face of a cube. The cube has six faces, and the charge q is located at the center of the cube, above the square face.
According to Gauss's law, the total electric flux Φ through a closed surface is given by:
Φ=qencϵ0
where qenc is the charge enclosed by the surface and ϵ0 is the permittivity of free space.
Since the charge q is at the center of the cube, the total electric flux through the entire surface of the cube is:
Φtotal=qϵ0
Since the cube has six faces and the charge is symmetrically placed, the flux will be evenly distributed among the six faces. Therefore, the flux through one face (which is our square) is:
Φsquare=Φtotal6=q6ϵ0
Thus, the electric flux through the square is:
Φ=q6ϵ0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Match the columns
5 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - All Questions
135 Videos
Similar Questions
A point charge of +6μC is placed at a distance 20 cm directly above the centre of a square of side 40 cm . The magnitude of the flux through the square is
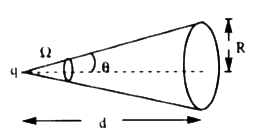
View SolutionA point charge q is placed at a distance d from the centre of a circular disc of radius R. Find electric flux flowing through the disc due to that charge
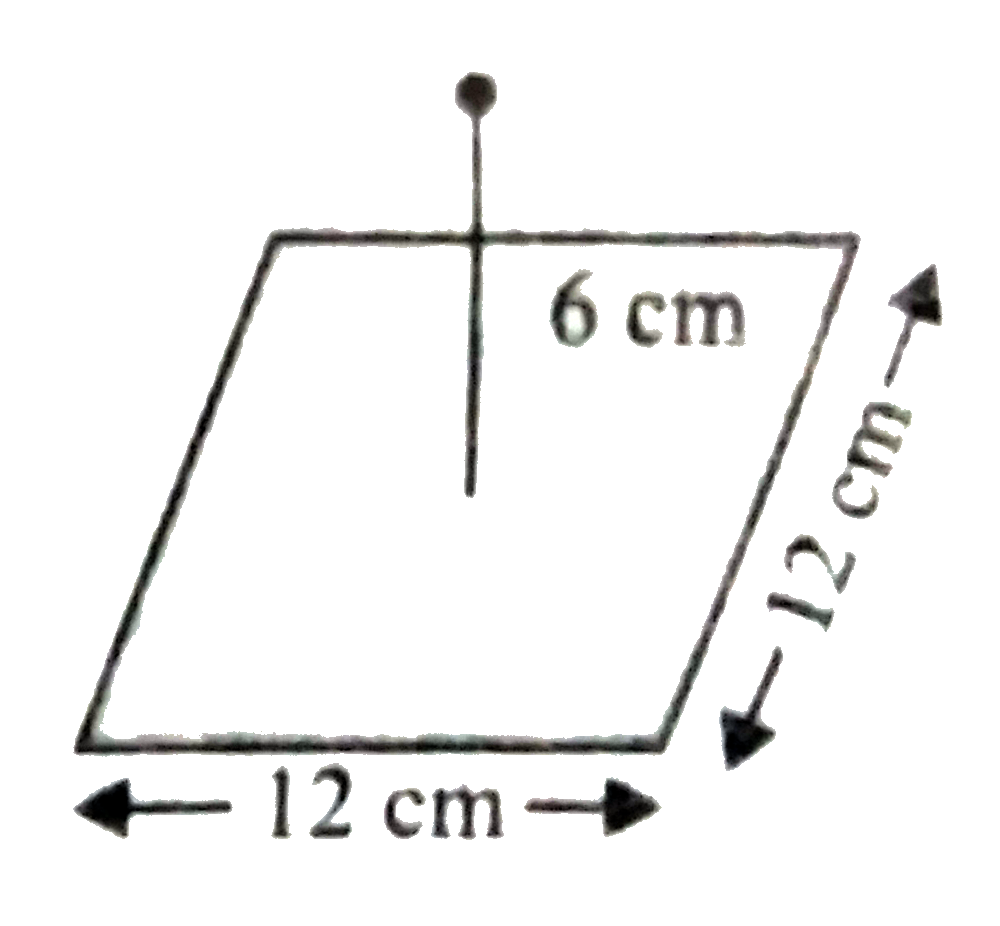
View SolutionA point charge +20muC is at a distance 6 cm directly above the centre of a square of side 12 cm as shown is figure. The magnitude of electric flux through the square is
View SolutionDefine electric flux. Is is the scalar or a vector quantity?
A point charge q is at a distance of d/2 directly above the centre of a square of side d, as shown in the figure. Use Gauss's law to obtain the expression for the electric flux through the square.
View SolutionA position charge Q is placed at a distance of 4R above the centre of a disc of radius R. The magnitude of flux through the disc is ϕ. Now a hemispherical shell of radius R is placed over the disc such that it forms a closed surface. The flux through the curved surface (taking direction of area vector along outward normal as positive), is -

View SolutionA point charge Q is placed at the corner of a square of side a. Find the flux through the square.
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
View SolutionA charge q is located at the centre of a cube. The electric flux through any face is
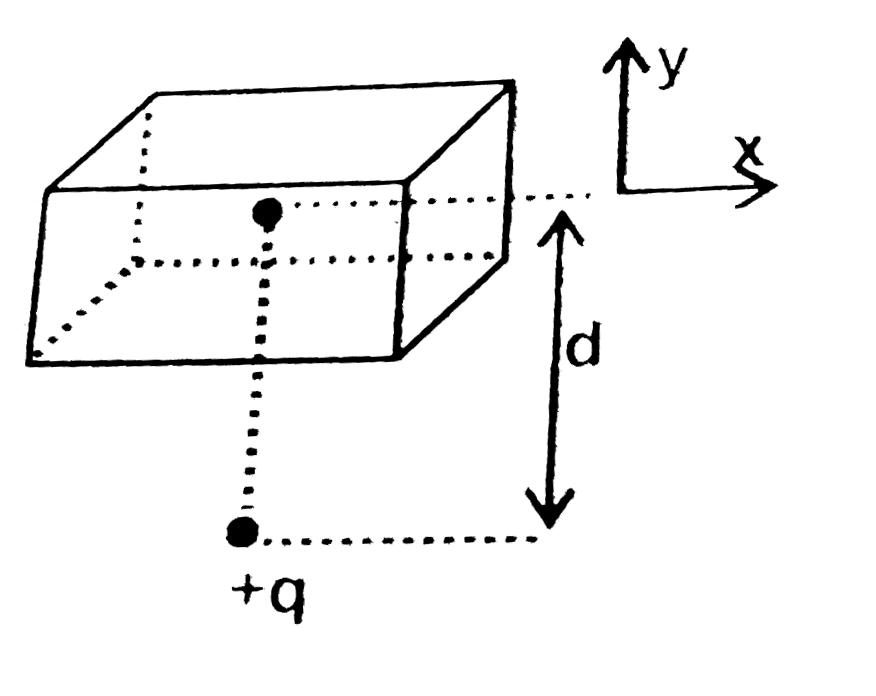
View SolutionA charge +q is placed at a distance 'd' from the centre of the uncharged metallic cube of side 'a'. The electric field at the centre of the cube due to induced charges on the cube will be
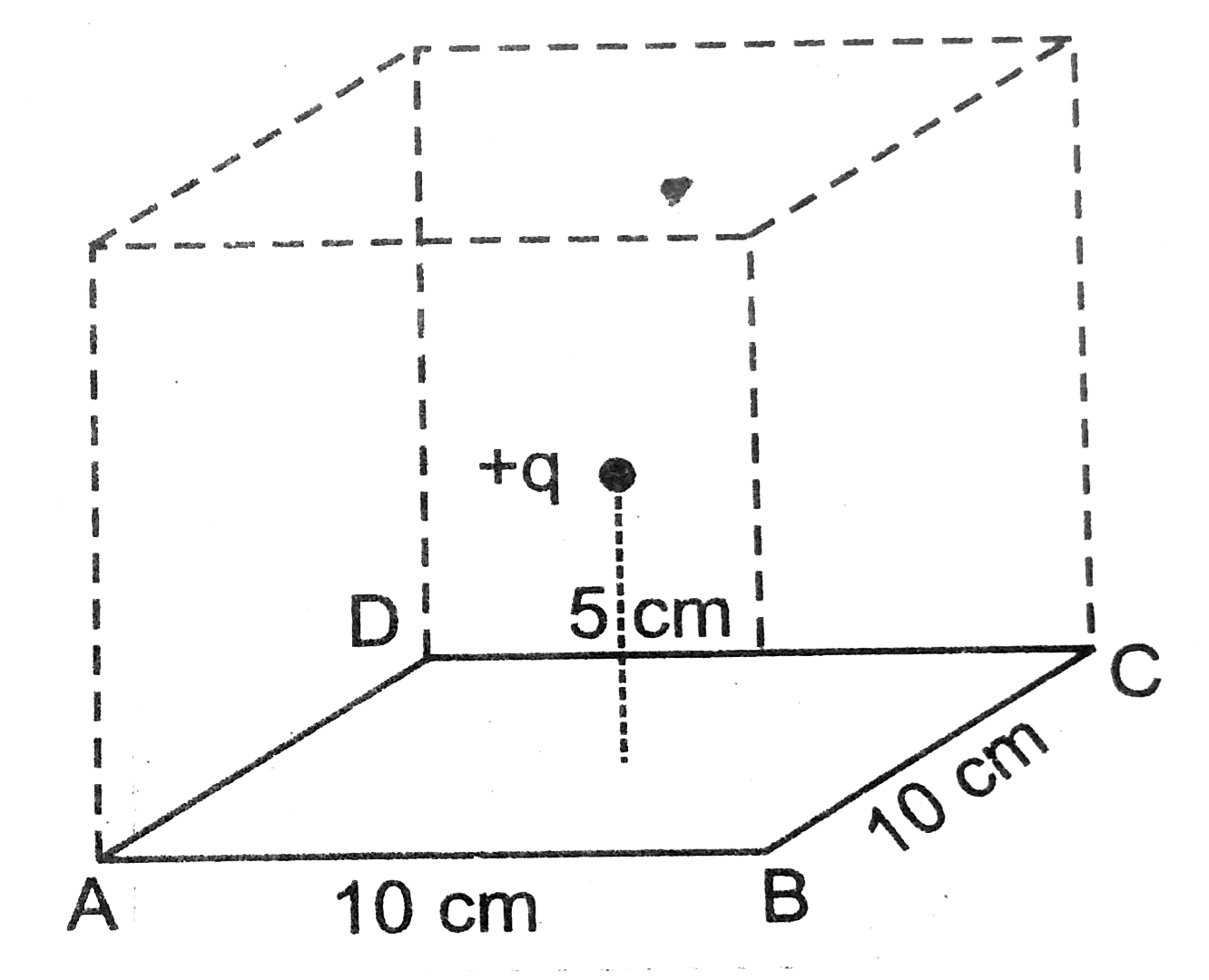
View SolutionA point charge +10μC is at distance of 5cm directly above the center of a square of side 10 cm as shown in Fig. What is the magnitude of the electric flux through the square ? (Hint. Think of the square of the square as one face of a cube with edge 10 cm)
View Solution
