It is not convenient to use a spherical Gaussian surface to find the electric field due to an electric dipole using Gauss's theorem because:
Gauss's law fails in this case
This problem does not have spherical symmetry
Coulomb's law is more fundamental than Gauss's law
Spherical Gaussian surface will alter the dipole moment
The correct Answer is:B
Similar Questions
Knowledge Check
Electric field due to an electric dipole is
Aspherically symmetricBcylindrical symmetricCasymmetricDnone of the aboveElectric field due to an electric dipole is
Aspherically symmetricBcylindrical symmetricCasymmetricDnone of the aboveThe Gaussian surface for calculating the electric field due to a charge distribution is
Aany closed surface around the charge distributionBany surface near the charge distributionCa spherical surfaceDa closed surface at a every point of which electric field has a normal components which is zero or a fixed value
Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.
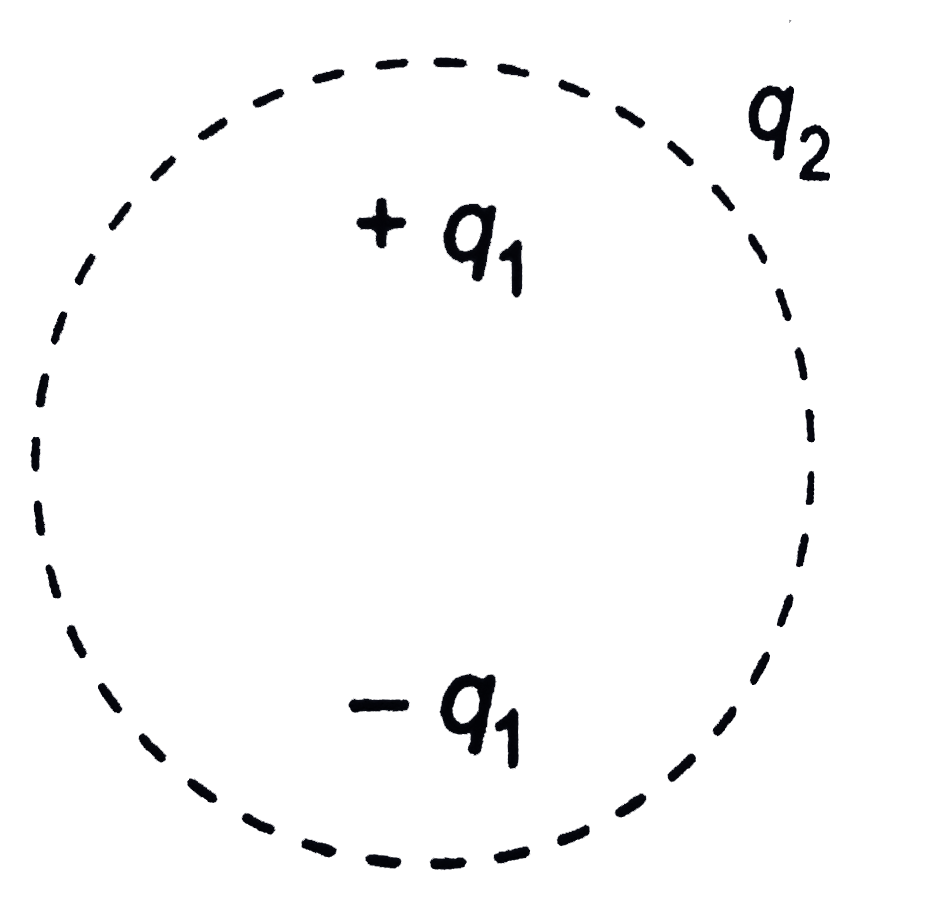
View SolutionConsider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.

View SolutionThe Gaussian surface for calculating the electric field due to a charge distribution is
View SolutionThe Gaussian surface needed for calculating the electric field due to a charge distribution is
View SolutionA : Gauss theorem is applicable on any closed surface.
R : In order to find the value of electric field due to a charge distribution, Gauss' theorem should be applid on a symmetrical closed surface.
View Solution
