Consider the charge configuration and a spherical Gaussian surface as shown in the figure. When calculating the flux of the electric field over the spherical surface, the electric field will be due to.

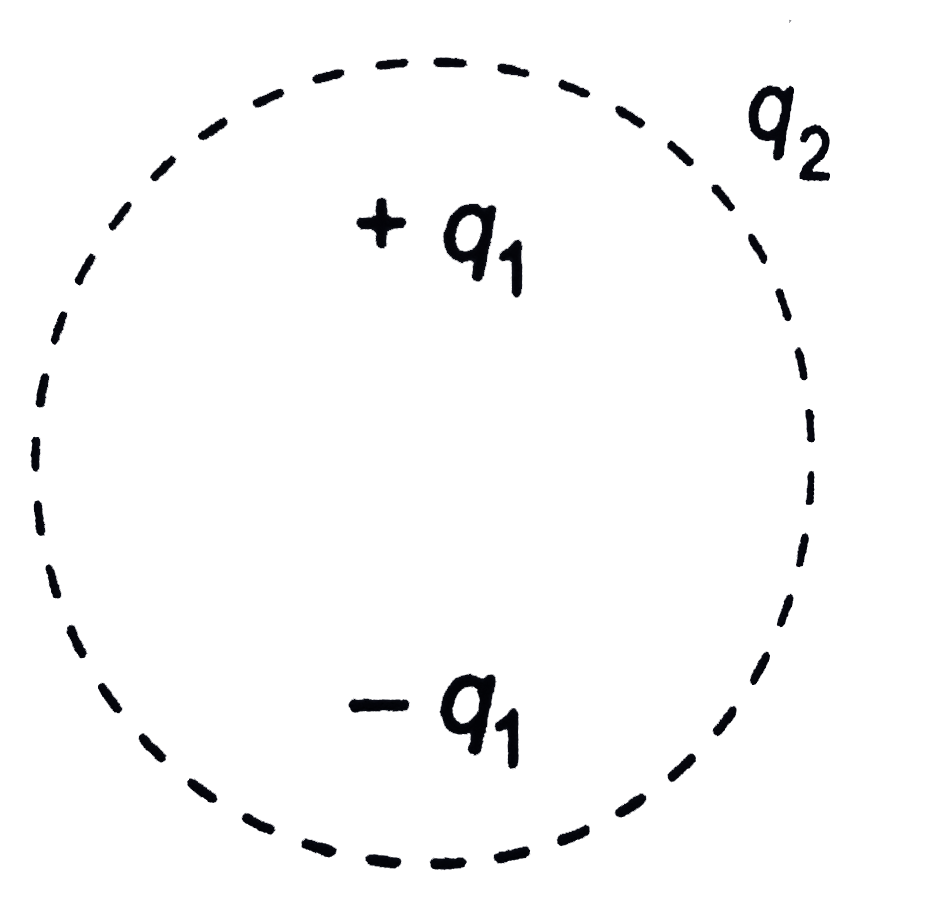
A

$q_{2}$

B

only the positive charges

C

all the charges

D

$+ q_{1}$ and $- q_{1}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

At any point over the spherical Gaussian surface, net electric field is the vector sum of electric fields due to $= q_{1}, q_{1}$ and $q_{2}$

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

The flux of electric field due to these charges through the surface S is

A $\frac{2 q}{ε_{0}}$
B $\frac{3 q}{ε_{0}}$
C $\frac{- 5 q}{ε_{0}}$
D $q ε_{0}$
A Gausisan surface in the figure is shown by dotted line.
The electric field on the surface will be

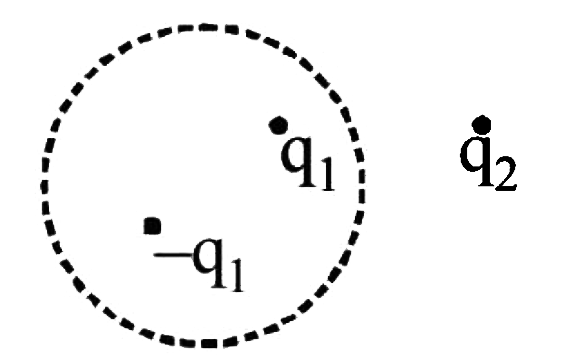A(a) due to $q_{1}$ and $q_{2}$ only
B(b) due to $q_{2}$ only
C(c) $z e r o$
D(d) due to all
Some equipotential surfaces are shown in figure . The magnitude and direction of electric field is

A $2 V / c m$ at angle $120^{\circ}$ with $+ v e$ x-axis in anticlockwise direction
B $2 V / c m$ at angle $120^{\circ}$ with $+ v e$ x-axis in clockwise direction
C $1 V / c m$ at angle $150^{\circ}$ with $+ v e$ x-axis in anticlockwise direction
D $1 V / c m$ at an angle $120^{\circ}$ with $+ v e$ x-axis in clockwise direction

DC PANDEY-ELECTROSTATICS-Level 2 Single Correct

Home
Ask Doubt
Profile