Refer to the arrangement of charged in and a Gaussian surface of radius R with Q at the centre. Then

A

total flux through the surface of the sphere is $\frac{+ Q}{ε_{0}}$

B

field on the surface of the spheres is $\frac{- Q}{4 π ε_{0} R^{2}}$

C

flux through the surface of sphere due to $5 Q$ is zero

D

field on the surface of sphere due to - 2Q is same everywhere

Text Solution

Verified by Experts

The correct Answer is:C

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROSTATICS

Similar Questions

Refer to the arrangement of charges in Fig and a Gaussian surface of radius $R$ with $Q$ at the centre. Then

View Solution
Can charge lie on a Gaussian surface?
View Solution

Knowledge Check

Question 1 - Select One or More
Refer to the arrangement of charges in Fig and a Gaussian surface of radius $R$ with $Q$ at the centre. Then

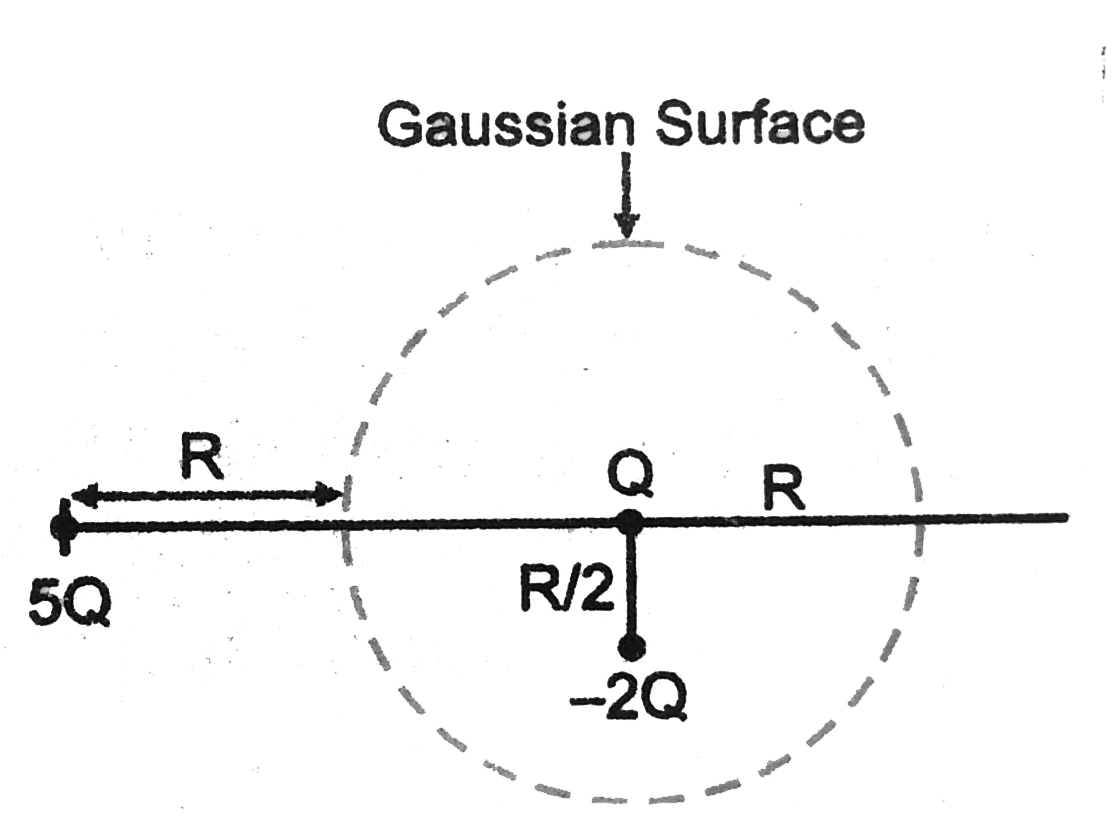Atotal flux through the surface of the sphere is $\frac{- Q}{\in_{0}}$
Bfield on the surface of the sphere si $\frac{- Q}{4 π \in_{0} R^{2}}$
Cflux through the surface of sphere due to $5 Q$ is zero.
Dfield on the surface of sphere due to $- 2 Q$ is same everywhere
Question 2 - Select One
The work done in carrying a charge q once round a circle of radius r with a charge Q at the centre is
A $\frac{q Q}{4 π ε_{0} a}$
B $\frac{q Q}{4 π ε_{0} a^{2}}$
C $\frac{q}{4 π ε_{0} a}$
Dzero
Question 3 - Select One
The work done in carrying a charge q once around a circle of radius r with a charge Q placed at the centre centre will be
A $\frac{Q q}{4 π ε_{0} r^{2}}$
B $\frac{Q q}{4 π ε_{0} r}$
Czero
D $\frac{Q q^{2}}{4 π ε_{0} r}$

Recommended Questions

Home
Ask Doubt
Profile