A small fish 0.4m below the surface of a lake is viewed through a simple converging ends of focal length 3m. The lens is kept at 0.2m above the water surface such that fish lies on the optical axis of the lens. The image of the fish seen by observer will be at (μwater=43)

A distance of 0.2m from the water surface
A distance of 0.6m from the water surface
A distance of 0.3m from the water surface
The same location of fish
The correct Answer is:D
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) STRAIGHT OBJECTIVE TYPE QUESTIONS ))10videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERICSE-III (LEVEL-II (ADVANCED) MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ))2videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - GEOMETRICAL OPTICSEXERCISE - PRACTICE SHEET (EXERICSE-II (LEVEL-II (ADVANCED) INTEGER TYPE QUESTIONS))5videos
GEOMETRICAL OPTICS
- BOOK - AAKASH SERIESCHAPTER - ELEMENTS OF VECTORSEXERCISE - QUESTIONS FOR DESCRIPTIVE ANSWERS9videos
ELEMENTS OF VECTORS
- BOOK - AAKASH SERIESCHAPTER - LAWS OF MOTIONEXERCISE - PRACTICE EXERCISE98videos
LAWS OF MOTION
Similar Questions
A small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m.the lens is kep at 0.2 m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observed. (μwater=43)
View SolutionA small fish 0.4 m below the surface of a lake is viewed through a simple converging lens of focal length 3 m.the lens is kep at 0.2 m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observed. (μwater=43)
View Solution
Knowledge Check
- Question 1 - Select One
The focal length of a lens is -0.4m. The lens is
AconvexBconcaveCcylindricalDnone of these
A small fish, 0.4m below the surface of a lake, is viewed through a simple converging lens of focal length 3m. The lens in kept at 0.2m above the water surface such that the fish lies on the optical axis of the lens. Find the image of the fish seen by the observer. The refractive index of water is 4/3.
View SolutionA small fish 0.4m below the surface of a lake, is viewed through a simple converging lens of focal length 3m. The lens is kept at 0.2m above the water surface such that the fish lies on the optical axis of the lens. Find the distance of the image of the fish from the lens as seen by the observer. The refractive index of water is 4/3.
View SolutionA stationary observer O looking at a fish F in water (μw=4/3) through a converging lens of focal length 90.0cm . The lens is allowed to fall frelly from a height 62.0cm with its axis vertical. The fish and the observer are on the principal axis of the lens. The fish moves up with constant velocity 100cm/s. Initially it was at depth of 44.0cm . Find the velocity (in cm//s) with which the fish appears to move with respect to lens to the observer at t=0.2s. (take g=10m/s2)
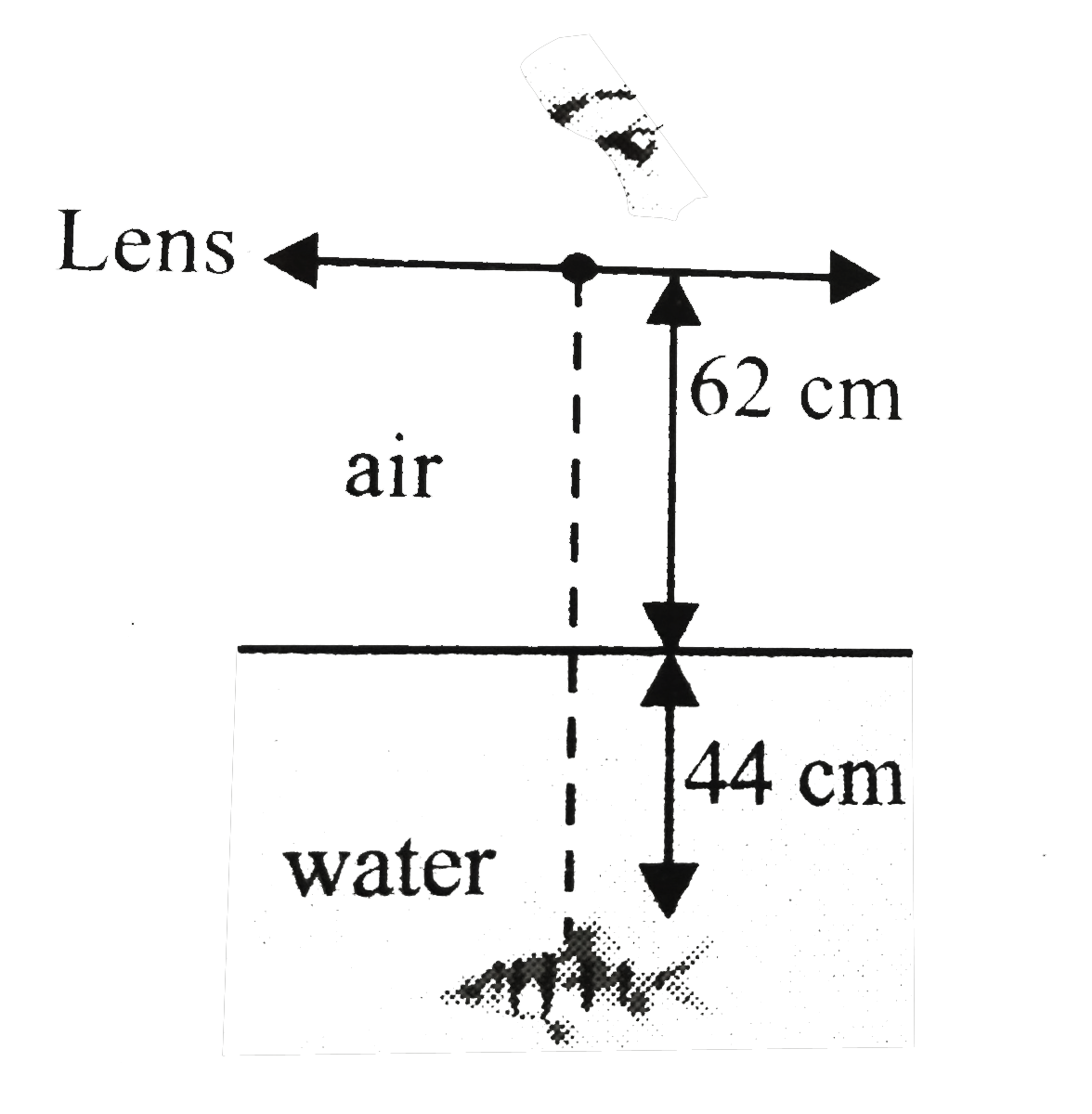 View Solution
View SolutionA stationary observer O looking at a fish F in water (μw=4/3) through a converging lens of focal length 90.0cm . The lens is allowed to fall frelly from a height 62.0cm with its axis vertical. The fish and the observer are on the principal axis of the lens. The fish moves up with constant velocity 100cm/s. Initially it was at depth of 44.0cm . Find the velocity (in cm//s) with which the fish appears to move with respect to lens to the observer at t=0.2s. (take g=10m/s2)
 View Solution
View SolutionAn object is kept at 0.2m from a convex lens of focal length 0.15 m. Find the position of the image produced.
View SolutionAn object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of 5m/s the speed and direction of the image will be :
View SolutionAn object is at a distance of 20 m form a convex lens of focal length 0.3m The lens forms an image of the object moves away form the lens at a speed of 5m/s the speed and direction of the image will be :
View Solution
