a particle moving in a circle track is given potential energy $U = - \frac{k}{r}$ where U is potential energy and r is radius. The correct graph between speed and radius of particles will be

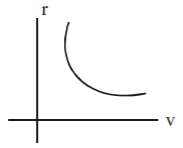
ocr_image

Video Solution

Text Solution

Generated By DoubtnutGPT

To solve the problem, we need to analyze the relationship between the speed of a particle moving in a circular track and its radius when the potential energy is given by $U = - \frac{k}{r}$ .
1. Understand the Potential Energy:
The potential energy of the particle is given as:
$U = - \frac{k}{r}$
where $k$ is a constant and $r$ is the radius of the circular path.
2. Calculate the Force:
The force acting on the particle can be derived from the potential energy using the relation:
$F = - \frac{d U}{d r}$
Calculating the derivative:
$F = - \frac{d}{d r} (- \frac{k}{r}) = \frac{k}{r^{2}}$
3. Centripetal Force Requirement:
For a particle moving in a circular path, the centripetal force required is given by:
$F_{c} = \frac{m v^{2}}{r}$
where $m$ is the mass of the particle and $v$ is its speed.
4. Set the Forces Equal:
Since the force derived from the potential energy must equal the centripetal force, we have:
$\frac{m v^{2}}{r} = \frac{k}{r^{2}}$
5. Rearranging the Equation:
Multiply both sides by $r$ :
$m v^{2} = \frac{k}{r}$
Now, solve for $v^{2}$ :
$v^{2} = \frac{k}{m r}$
6. Express Speed in Terms of Radius:
Taking the square root gives us the expression for speed:
$v = \sqrt{\frac{k}{m}} \cdot \frac{1}{\sqrt{r}}$
This shows that speed $v$ is inversely proportional to the square root of the radius $r$ .
7. Graph Interpretation:
The relationship $v \propto \frac{1}{\sqrt{r}}$ indicates that as the radius increases, the speed decreases. This relationship will produce a hyperbolic curve when plotted on a graph of speed $v$ versus radius $r$ .
Conclusion:
The correct graph between speed and radius of the particle will be a hyperbolic curve.

Updated on:18/9/2024