A right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______Solution in Telugu
The correct Answer is:9
Step by step video & text solution for A right triangle is drawn in a semicircle of radius (1)/(2) with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32sqrt(3)Mc is _______ by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - I (MAIN)) (STRAIGHT OBJECTIVE TYPE QUESTIONS)
50 Videos
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)
10 Videos
- MAXIMA AND MINIMA BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II) (LINKED COMPREHENSION TYPE QUESTIONS )
6 Videos
- MAXIMA & MINIMABOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III
35 Videos
- MEAN VALUE THEOREMSBOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )
2 Videos
Similar Questions
The minimum value of (A2+A+1)(B2+B+1)(C2+C+1)(D2+D+1)BACD , wher A,B,C,D are positive
View SolutionLet f(x)=(x−1)4(x−2)n, n in N.. Then f(x) has
View SolutionIf f11(x)<0(>0) on an interval (a,b) then the curve y=f(x) on this interval is convex (concave) i.e it is below (above) any of its tangent lines If f11(x0)=0 or does not exist and the second derivative changes sign when passing through the point x0 then the point (x0,f(x)) is the = point of inflection of the curve y=f(x)
If y=x4+x3−18x2+24x−12 then
View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )
View SolutionIn a right triangle ABC ,right angled at A, on the leg AC as diameter,a semicircle is described.The chord joining A with the point of intersection D of the hypotenuse and the semicircle,then the length AC equals to
View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionA right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter. If the maximum area of the triangle is M , then the value of 32√3Mc is______
View SolutionIn a Delta ABC, a semicircle is inscribed,whose diameter lies on the side c.Then the radius of the semicircle is (Where Delta is the area of the triangle ABC)
View Solutionत्रिज्या r के एक अर्द्धवृत्त के अन्दर खींचे जा सकने वाले सबसे बड़े त्रिभुज का क्षेत्रफल ज्ञात कीजिए।
View SolutionThe area of a right triangle is 40cm2. If one of its legs measures 8 cm, find the length of the other leg.
View SolutionThe legs of a right triangle are in the ratio 3 : 4 and its area is 1014cm2 . Find the lengths of its legs.
View SolutionIn Fig 12.58, ABC is a triangle right angled at A. Semicircles are drawn on AB and AC as diameters. Find the area of the shaded region.
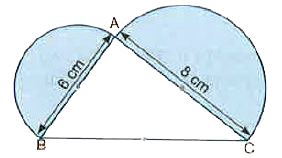
View SolutionABC is a right-angled triangle at A. Semicircles drawn on AB, AC and BC as diameters. Find area of the shaded region.

View SolutionProve that the area of the semicircle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the semicircles drawn on the other two sides of the triangle
View SolutionA right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter. If the maximum area of the triangle is M , then the value of 32√3Mc is______
View Solution
