f(x)=|xlogex|monotonically decreases in Solution in Telugu
(0,1/e)
(1e,1)
(1,∞)
(−∞,1)
The correct Answer is:B
Step by step video & text solution for f(x)=|xlog_(e )x|monotonically decreases in by Maths experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS)10videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - ADDITIONAL PRACTICE EXERCISE (LEVEL - II (LECTURE SHEET )(ADVANCED)) (MATRIX MATCHING TYPE QUESTIONS)2videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA AND MINIMA EXERCISE - PRACTICE SHEET (EXERCISE -II) (LEVEL -II)(INTEGER TYPE QUESTIONS)4videos
MAXIMA AND MINIMA
- BOOK - AAKASH SERIESCHAPTER - MAXIMA & MINIMAEXERCISE - EXERCISE-III35videos
MAXIMA & MINIMA
- BOOK - AAKASH SERIESCHAPTER - MEAN VALUE THEOREMSEXERCISE - PRACTICE SHEET (EXERCISE-I (LEVEL-II (MORE THAN ONE CORRECT ANSWER TYPE QUESTIONS ) )2videos
MEAN VALUE THEOREMS
Similar Questions
Let f(x)=(x−1)4(x−2)n, n in N.. Then f(x) has
03:32View SolutionThe function f(x)=√(ax3+bx2+cx+d) has its nonzero local minimum an d maximum values at x=-2 andx=2 , repectively . If a is a root of x2−x−x6=0 , then match the following
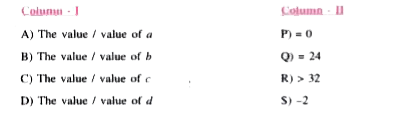 03:02View Solution
03:02View SolutionA right triangle is drawn in a semicircle of radius 12 with one of its legs along the diameter . If the maximum area of the triangle is M , then the value of 32√3Mc is _______
02:18View SolutionThe maximum slope of the curve y=−x3+3x2+9x−27 is
01:28View SolutionGiven f(x) = 4- ((1)/(2) - x)^(2//3) , g(x) = {:{((tan[x])/(x),","x cancel(=)0),(1,","x=0):}" "h(x)={x}, k (x) = 5^(log_(2)(x+3))
Then in [0,1], Lagrange's mean value theorem is not applicable to (where [.] and {.} represents the greatest integer functions and fractions part functions, respectively )02:41View SolutionIf a<0, the function f(x)=e^(ax)+e^(-ax) is a monotonically decreasing function for values of x given by
04:26View SolutionIf a<0 and f(x)=eax+e−ax is monotonically decreasing . Find the interval to which x belongs.
02:47View SolutionThe function f(x)=cos x -2 px is monotonically decreasing for
View SolutionThe function f(x)=cosx−2ax is monotonically decreasing when-
03:13View SolutionIf xy=ax,prove that dydx=xlogea−yxlogex.
03:23View Solutionf(x)=x5−20x3+240x, then f(x) is
O Monotonically decreasing everywhere
O Monotonically decreasing on (0,∞)
O Monotonically increasing on (−∞,0)
O Monotonically increasing everywhere04:07View Solutionf(x)=cosx−2ax monotonically decreases when
04:03View Solutionf(x) = |xlogx|,x>0 is monotonically decreasing in
01:49View Solutionf(x)=|xlogex| monotonically decreases in (0,1e) (b) (1e,1) (1,∞) (d) (1e,∞)
03:28View SolutionIf a<0, the function f(x)=eax+e−ax is a monotonically decreasing function for values of x given by
02:35View Solution

