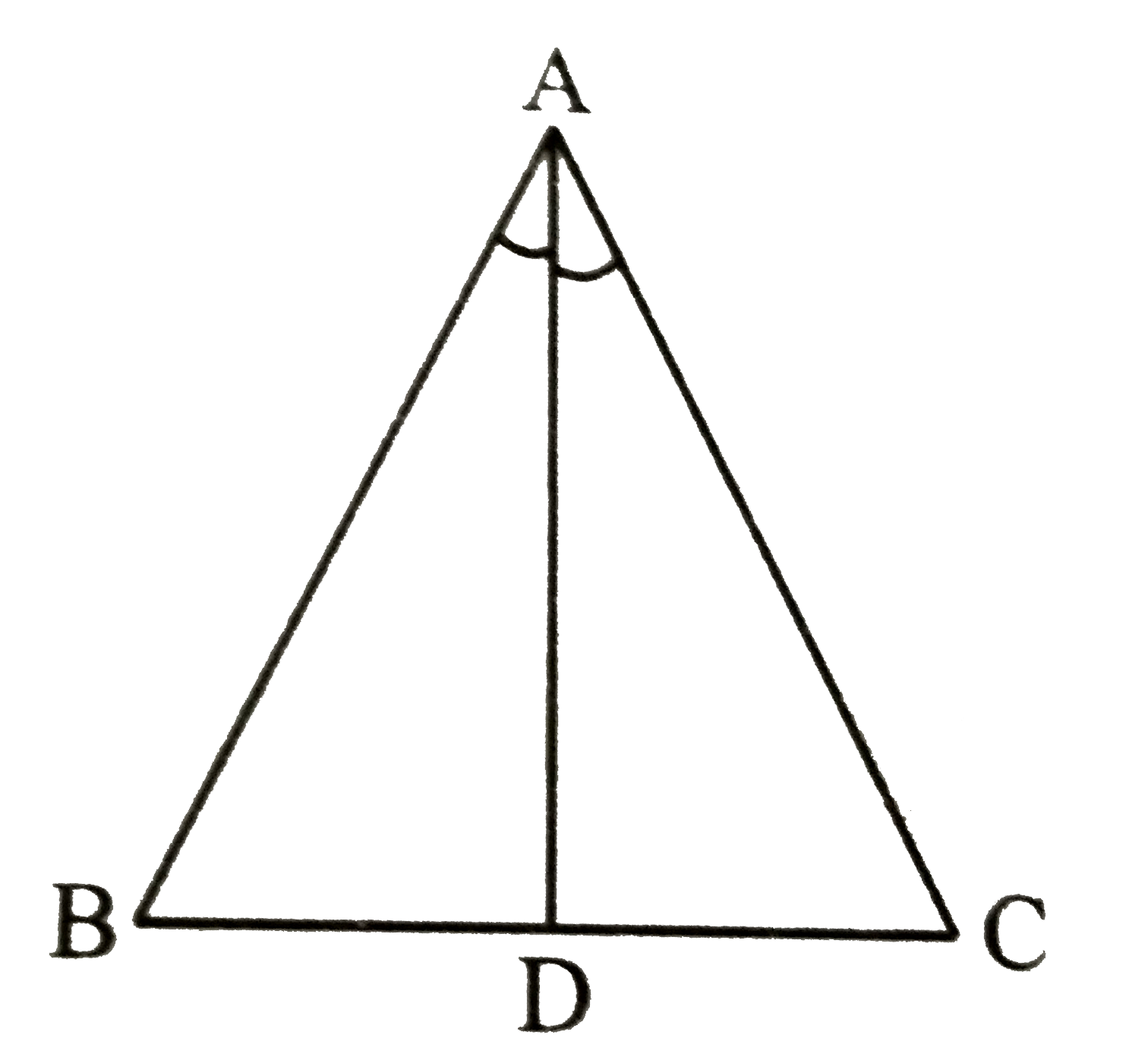
Prove:In a triangle the angle bisector divides the side opposite to the angle in the ratio of the remaining sides.Solution in Marathi
Step by step video & image solution for Prove:In a triangle the angle bisector divides the side opposite to the angle in the ratio of the remaining sides. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
Similar Questions
If in △ABCand△PQR for some one-one correspondence if ABQR=BCPR=CAPQ then: a)△PQR~△ABC b)△PQR~△CAB c)△CBA~△PQR d)△BCA~△PQR
04:30View SolutionIf A={1,3,5},B{2,4,6} then A∩B=?
12:58View SolutionFind the median of the data 54,63,66,72,98,87,92.
05:10View SolutionThe internal angle bisector of an angle of a triangle divide the opposite side internally in the ratio of the sides containgthe angle
01:11View SolutionThe external angle bisector of an angle of a triangle divides the opposite side externally in the ratio of the sides containing the angle.
01:54View SolutionIf one angle of a triangle is equal to one angle of another triangle and bisector of these equal angles divide the opposite side in the same ratio; prove that the triangles are similar.
02:36View SolutionIf the bisector of an angle of a triangle bisects the opposite side, prove that the triangle is isosceles.
05:04View SolutionIf in ΔABC, the difference of two angles is 600 and the remaining angle is 300, then find the ratio of the sides opposite to first two angles.
02:57View SolutionOne angle of a triangle is equal to one angle of another triangle and the bisectors of these two equal angles divide the opposite sides in the same ratio, prove that the triangles are similar.
04:55View Solutionयदि किसी त्रिभुज के एक कोण का समद्विभाजक सम्मुख भुजा को समद्विभाजित करता हो , तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु त्रिभुज है ।
05:10View Solutionयदि एक त्रिभुज के एक कोण का अर्द्धक, विपरीत भुजाओं का अर्द्धक है तो सिद्ध कीजिए कि त्रिभुज समद्विबाहु है ।
 10:09View Solution
10:09View SolutionIn order to prove, 'The bisector of an angle of a triangle divides the side opposite to the angle in the ratio of the remaining sides.
(i) Draw a neat labelled figure.
(ii) Write 'Given' and 'To prove'.View SolutionProve the following statement. "The bisector of an angle of a triangle divides the sides opposite to the angle in the ratio of the remaining sides"
04:55View SolutionAtempt any two of the following :
Prove : In a triangle the angle bisector divides the side opposite to the angle in the ratio of the remaining sides.06:06View SolutionThe ………….. of an angle of a triangle divides the opposite side internally in the ratio of the corresponding sides containing the angle.
05:29View Solution

