Consider that an ideal gas (n moles) is expanding in a process given by P=f(V), which passes through a point (V0,P0). Show that the gas is absorbing heat at (P0,V0) if the slope of the curve P=f(V) is larger than the slope of the adiabat passing through (P0,V0).
Slope of P=f(V), curve at (V0,P0)=f(V0)
Slope of adiabat at (V0P0)
=k(−γ)V−1−γ0=−γP0/V0
Now heat absorbed in the process P = f(V)
dQ=dU+dW=nCvdT+PdV
Since T=(1/nR)PV=(1/nR)Vf(V)
dT=(1/nR)[f(V)+Vf.(V)]dV
Thus dQdV V=V0=CVR[f(V0)+V0f.(V0)]+f(V0)
=[1γ−1+1]f(V0)+V0f.(V0)γ−1
=γγ−1P0+V0γ−1f.(V0)
Heat is absorbed when dQ/dV>0 when gas expands, that is when
γP0+V0f.(V0)>0
f.(V0)>−γP0/V0
Similar Questions
Consider that an ideal gas (nmoles) is expanding in a process given by P=f(V), which passes through a point (P0,V0). Show that the gas is absorbing heat at (P0,V0) if the slope of the curve P=f(V) is larger than the slope of the adiabat passing through (p0,V0).
View SolutionConsider that an idela gas (n mole) is espanding in a process gives by p=f(v), which passes throught a point (V0,p0). Shown that the gas is absorbing heat at (p0,v0) if the slope of the curve p=f(v) is large than the slope of the adabatic passing throught (p0,v0).
View Solution
Knowledge Check
2 moles of ideal monatomic gas is carried from a state (P0,V0) to a state (2P0,2V0) along a straight line path in a P- V diagram. The amount of heat absorbed by
A3P0V0B92P0V0C6P0V0D32P0V0A monoatomic gas expands following as thermodynamic law P=C1V+C2, where C1,C2 are constants, from state A(V0,3P0) to B(3V0,P0).What will be the volume of the gas upto which it absorbs heat?
AV0B2V0C2.5V0D3V0An ideal monatomic gas is at P0,V0. It is taken to final volume 2V0 when pressure is P0/2 in a process which is straight line on P−V diagram. Then
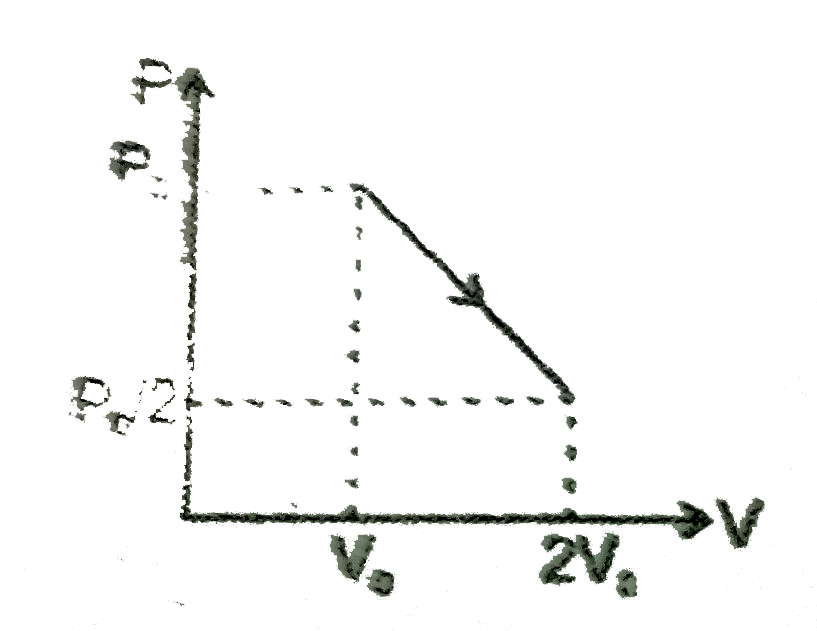 AThe final temperature is equal to initial temperatureBThere is no change in internal energyCThe work done by the gas is +P0V04DThe heat is absorbed in the process.
AThe final temperature is equal to initial temperatureBThere is no change in internal energyCThe work done by the gas is +P0V04DThe heat is absorbed in the process.
Consider that an idela gas (n mole) is espanding in a process gives by p=f(v), which passes throught a point (V0,p0). Shown that the gas is absorbing heat at (p0,v0) if the slope of the curve p=f(v) is large than the slope of the adabatic passing throught (p0,v0).
View Solutionn' moles of an ideal gas undergoes a process A→B as shown in the figure. The maximum temperature of the gas during the process will is p0v04nR then value of N is:
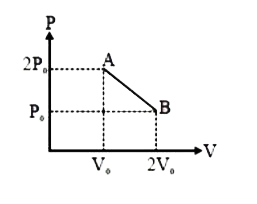
View SolutionAn ideal monatomic gas is at P0,V0. It is taken to final volume 2V0 when pressure is P0/2 in a process which is straight line on P−V diagram. Then

View SolutionThe internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
What is the value of γ(=CP/CV) for the given gas?
View SolutionThe internal energy of a gas is given by U = 3 pV. It expands from V0 to 2V0 against a constant pressure p0.
What is the value of γ(=CP/CV) for the given gas?
View Solution
