Suppose f(x)=(x+1)2 for x≥−1. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y=x, then g(x) equals
1−√x−1,x≥0
1(x+1)2,x>−1
√x+1,x≥−1
√x−1,x≥0
The correct Answer is:D
Similar Questions
Suppose f(x)=(x+1)2 forx≥−1. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y=x, then g(x) equal. (a)1−√x−1,x≥0 (b) 1(x+1)2,x>−1 (c)√x+1,x≥−1 (d) √x−1,x≥0
View SolutionSuppose f(x)=(x+1)2 forx≥−1. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y=x, then g(x) equal. (a)1−√x−1,x≥0 (b) 1(x+1)2,x>−1 (c)√x+1,x≥−1 (d) √x−1,x≥0
View Solution
Knowledge Check
If g(x)=x-2 is the inverse of the function f(x)=x+2, then graph of g(x) is the image of graph of f(x) about the line y=kx. Here k =
A1B2C3D4
Suppose f(x)=(x+1)2forx≥−1. If g(x) is the function whose graph is the reflection of the graph of f(x) with respect to the line y=x, then g(x) equal. a−√x−1,x≥0 (b) 1(x+1)2,x≻1 √x+1,x≥−1 (d) √x−1,x≥0
View SolutionThe function whose graph is the reflection about the line x+y=0 of the inverse function f−1 of a function f(x) is
View SolutionThe function whose graph is the reflection about the line x+y=0 of the inverse function f−1(x) of a function f(x) is
View SolutionIf the graph of the function y = f(x) is symmetrical about the line x = 2, then
View SolutionLet f:(−0,2]→[6,∞) be defined as f(x)=4x2–16x+22 and g(x) is a function such that graphs of f(x) and g(x) are mirror image of each other with respect to line x−y=0, then g(10) is equal to
View SolutionConsider the following function f whose graph is given below.
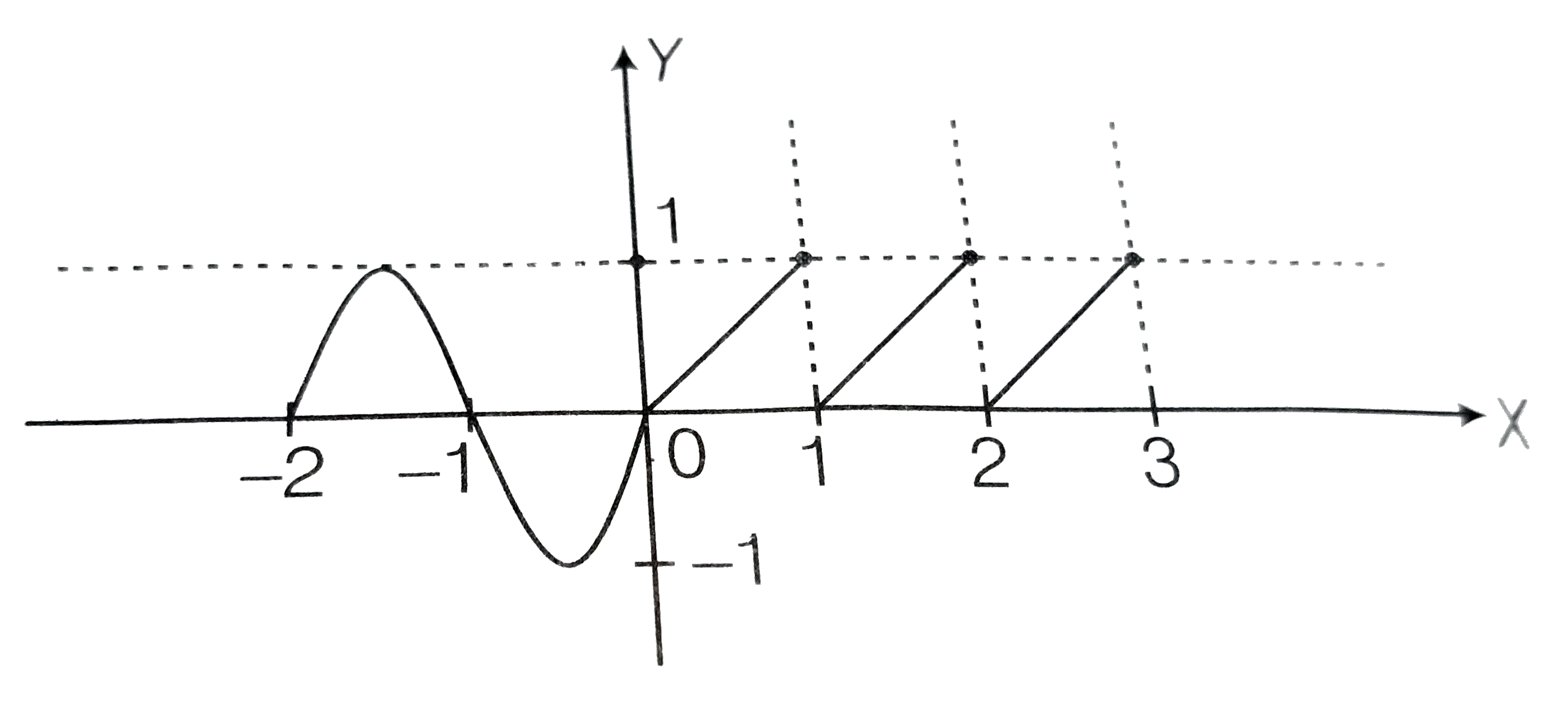
Draw the graph of following functions.
(g) 2f(x)
View SolutionConsider the following function f whose graph is given below.

Draw the graph of following functions.
(g) 2f(x)
View Solution
