Let A(-1, 1), B(3, 4) and C(2,0) be given three points. A line y=mx,m>0, intersects lines AC and BC at point P and Q respectively. Let A1 and A2 be the areas of ΔABC and ΔPQC respectively, such that A1=3A2, then the value of m is equal to :
415
1
3
2
To solve the problem, we need to find the value of m such that the area of triangle ABC is three times the area of triangle PQC, where P and Q are the intersection points of the line y=mx with segments AC and BC respectively.
Step 1: Calculate the area of triangle ABC
The area A1 of triangle ABC can be calculated using the formula:
A1=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
where A(−1,1), B(3,4), and C(2,0).
Substituting the coordinates:
A1=12|−1(4−0)+3(0−1)+2(1−4)|
Calculating this:
=12|−4−3−6|=12|−13|=132
Step 2: Set up the relationship between the areas
Given that A1=3A2, we can express A2 as:
A2=A13=13/23=136
Step 3: Find the equations of lines AC and BC
Line AC:
The slope of line AC is:
slope=0−12−(−1)=−13
Using point-slope form:
y−1=−13(x+1)⟹y=−13x+23
Line BC:
The slope of line BC is:
slope=0−42−3=4
Using point-slope form:
y−4=4(x−3)⟹y=4x−8
Step 4: Find points P and Q
Point P (intersection of y=mx and AC):
Setting mx=−13x+23:
mx+13x=23⟹x(m+13)=23⟹x=23(m+13)
Substituting back to find y:
y=m⋅23(m+13)=2m3(m+13)
Point Q (intersection of y=mx and BC):
Setting mx=4x−8:
mx−4x=−8⟹x(m−4)=−8⟹x=−8m−4
Substituting back to find y:
y=m⋅−8m−4=−8mm−4
Step 5: Calculate the area of triangle PQC
Using the coordinates of P⎛⎝23(m+13),2m3(m+13)⎞⎠, Q(−8m−4,−8mm−4), and C(2,0):
A2=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Substituting the coordinates and simplifying leads to:
A2=12|determinant|
Step 6: Set up the equation A1=3A2
Substituting A1 and A2 into the equation and solving for m gives us the required value.
Final Step: Solve for m
After simplifying the resulting equation, we find that the positive value of m is:
m=1
A1=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
where A(−1,1), B(3,4), and C(2,0).
A1=12|−1(4−0)+3(0−1)+2(1−4)|
Calculating this:
=12|−4−3−6|=12|−13|=132
A2=A13=13/23=136
The slope of line AC is:
slope=0−12−(−1)=−13
Using point-slope form:
y−1=−13(x+1)⟹y=−13x+23
The slope of line BC is:
slope=0−42−3=4
Using point-slope form:
y−4=4(x−3)⟹y=4x−8
Setting mx=−13x+23:
mx+13x=23⟹x(m+13)=23⟹x=23(m+13)
Substituting back to find y:
y=m⋅23(m+13)=2m3(m+13)
Setting mx=4x−8:
mx−4x=−8⟹x(m−4)=−8⟹x=−8m−4
Substituting back to find y:
y=m⋅−8m−4=−8mm−4
A2=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Substituting the coordinates and simplifying leads to:
A2=12|determinant|
m=1
Topper's Solved these Questions
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - Mathematic section B10videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2021EXERCISE - MATHEMATICS SECTION B20videos
JEE MAIN 2021
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAINEXERCISE - QUESTION1videos
JEE MAIN
- BOOK - JEE MAINS PREVIOUS YEARCHAPTER - JEE MAIN 2022EXERCISE - Question454videos
JEE MAIN 2022
Similar Questions
If a1,a2,a3 are the last three digits of 17256 respectively then the value of a2−a1−a3 is equal
View SolutionLet a and b be two positive real numbers such that a+2b≤1. Let A1 and A2 be, respectively, the areas of circles with radii ab3 and b2. Then the maximum possible value of A1A2 is:
View Solution
Knowledge Check
- Question 1 - Select One
Consider 3 points A(-1,1) , B(3,4) and C(2,0) . The line y=mx+c cuts line AC and BC at points P and Q res. If the area of ΔABC=A1 and area of ΔPQC=A2 and A1=3A2 then positive value of m is
A1B415C2D154 - Question 2 - Select One
The spectrum of a black body at two temperatures 27∘C and 327∘C is shown in the figure. Let A1 and A2 be the areas under the two curves respectively. Find the value of A2A1
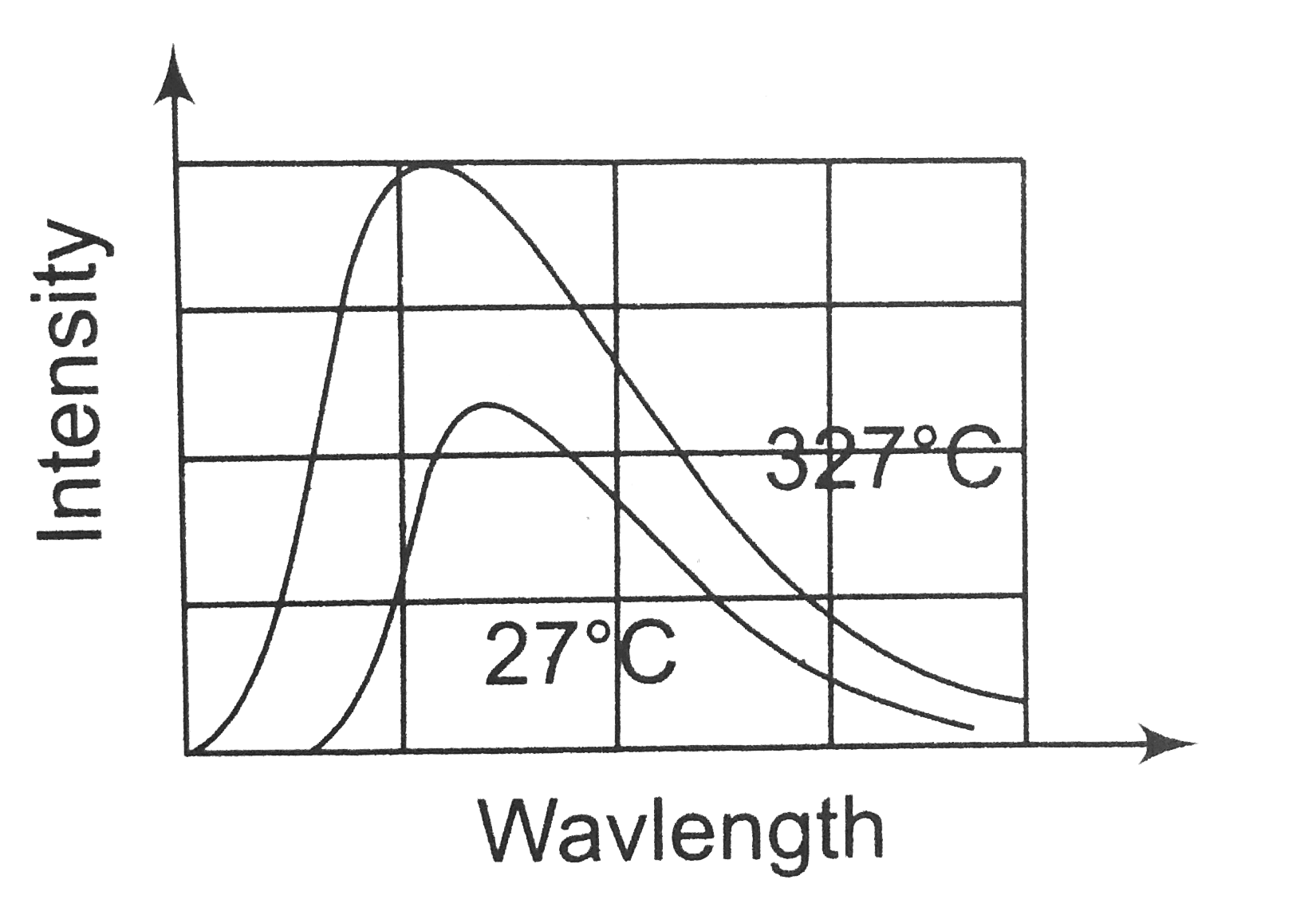 A16:1B8:1C9:4D16:9
A16:1B8:1C9:4D16:9 - Question 3 - Select One
Let points A1,A2andA3 lie on the parabola y2=8x. If △A1A2A3 is an equilateral triangle and normals at points A1,A2andA3 on this parabola meet at the point (h, 0). Then the value of h I s
A24B26C38D28
A1,A2 are two arithmetic means between two positive real numbers a and b. P is the point of intersection of the perpendicular lines 2x+y−20=0 and x−2y+10=0. If the centroid of the triangle with vertices (a,b),(A1,A2) and (A2,A1) lies at the point P, the value of ab is equal to
View SolutionThe line L1≡3x−4y+1=0 touches the circles C1andC2. Centers of C1 and C2 are A1(1,2) and A2(3,1) respectively Then, the length (in units) of the transverse common tangent of C1andC2 is equal to
View Solutionn equidistant points A1,A2,A3………An are taken on base BC of ΔABC is A1B=A1A2=AnC and area of ΔAA4A5 is k cm2, then what is the area of ΔABC.
View SolutionLet the straight line y=k divide the area enclosed by x=(1−y)2 , x=0 and y=0 into two parts of areas, A1(0≤y≤k) and A2(k≤y≤1) such that A1A2=7. Then 1k is equal to
View SolutionThe corresponding medians of two similar triangles are in the ratio 4:7. Let their respective areas be A1 and A2.A1:A2=…
View Solution

