Find out the surface charge density at the intersection of point x=3 m plane and x-axis, in the region of uniform line charge of 8 nC/m lying along the z-axis in free space.
47.88C/m
4.0nCm−2
0.07nCm−2
0.424nCm−2
To find the surface charge density at the intersection of the plane x=3m and the x-axis in the presence of a uniform line charge of 8nC/m along the z-axis, we can follow these steps:
Step 1: Understand the Problem
We have a uniform line charge density λ=8nC/m=8×10−9C/m located along the z-axis. We need to find the surface charge density σ at the plane x=3m.
Step 2: Electric Field Due to Line Charge
The electric field E due to an infinite line charge at a distance r from the line charge is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
Step 3: Determine the Distance
At the plane x=3m, the distance r from the line charge (which lies along the z-axis) to the plane is simply 3m.
Step 4: Calculate the Electric Field
Substituting the values into the electric field equation:
E=8×10−92π(8.85×10−12)(3)
Calculating this gives:
E=8×10−92π(8.85×10−12)(3)≈0.424N/C
Step 5: Relate Electric Field to Surface Charge Density
The surface charge density σ can be related to the electric field E at the surface by the equation:
σ=ϵ0E
Substituting E into this equation:
σ=(8.85×10−12)×(0.424)
Step 6: Calculate Surface Charge Density
Calculating σ:
σ≈3.75×10−12C/m2=0.375nC/m2
Final Answer
The surface charge density σ at the intersection of the plane x=3m and the x-axis is approximately 0.375nC/m2.
---
We have a uniform line charge density λ=8nC/m=8×10−9C/m located along the z-axis. We need to find the surface charge density σ at the plane x=3m.
The electric field E due to an infinite line charge at a distance r from the line charge is given by the formula:
E=λ2πϵ0r
where ϵ0 is the permittivity of free space, approximately 8.85×10−12C2/(N⋅m2).
At the plane x=3m, the distance r from the line charge (which lies along the z-axis) to the plane is simply 3m.
Substituting the values into the electric field equation:
E=8×10−92π(8.85×10−12)(3)
Calculating this gives:
E=8×10−92π(8.85×10−12)(3)≈0.424N/C
The surface charge density σ can be related to the electric field E at the surface by the equation:
σ=ϵ0E
Substituting E into this equation:
σ=(8.85×10−12)×(0.424)
Calculating σ:
σ≈3.75×10−12C/m2=0.375nC/m2
The surface charge density σ at the intersection of the plane x=3m and the x-axis is approximately 0.375nC/m2.
Similar Questions
A uniformly charged disc of radius R having surface charge density σ is placed in the xy plane with its center at the origin. Find the electric field intensity along the z-axis at a distance Z from origin :
View SolutionFind the electric flux due to a point charge 'Q' through the circular region of radius R if the charge is placed on the axis of ring at a distance x.
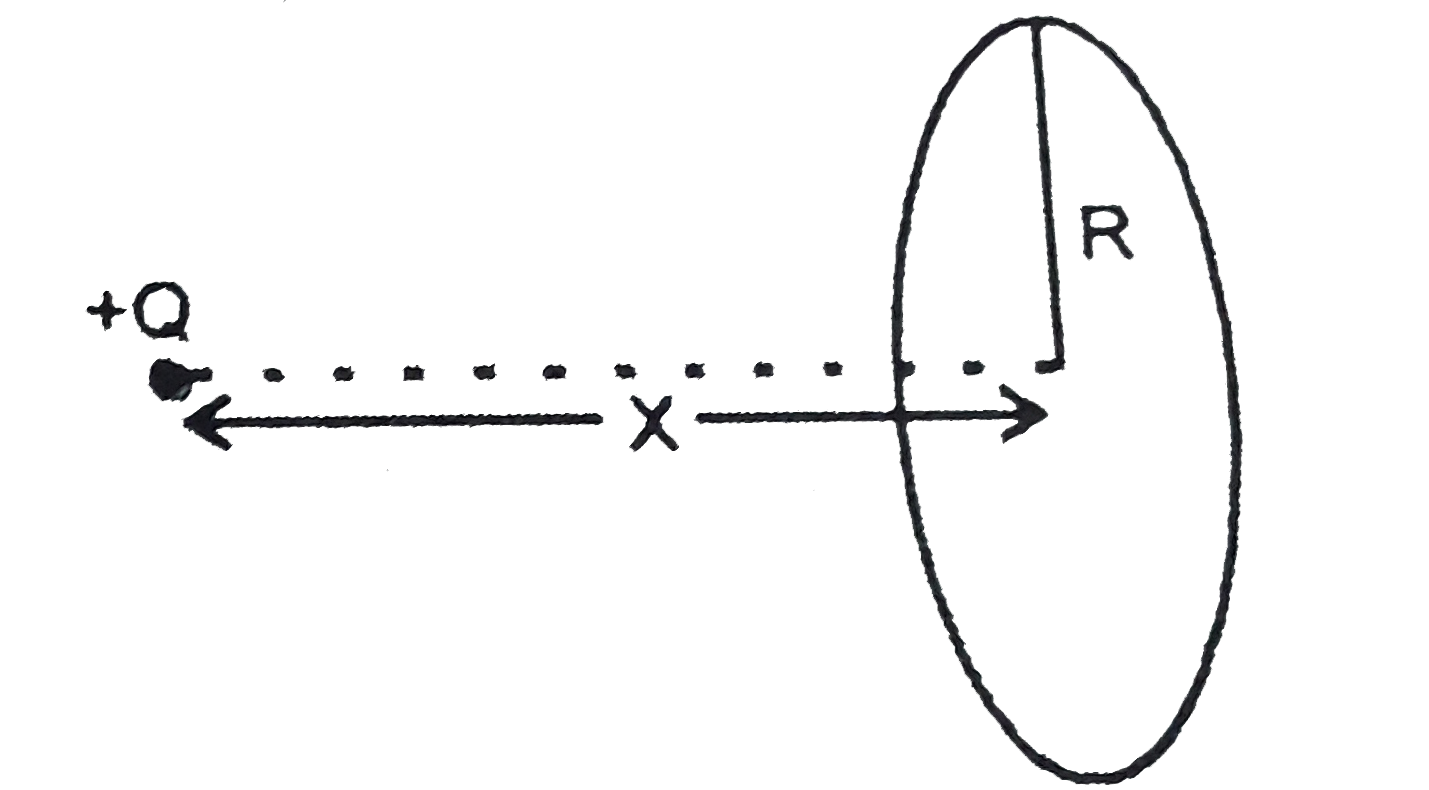
View Solution
Knowledge Check
A uniformly charged square plate having side L carries a uniform surface charge density σ. The plate lies in the y−z plane with its centre at the origin. A point charge q lies on the x-axis. The flux of the electric field of q through the plate is ϕ0, while the foce on the point charge q due to the plate is F0, along the x-axis. Then,
Aσ=F0ϕ0LBσ=F0ϕ0Cσ=F0Lϕ0Dσ=ϕ0F0Consider an infinite line charge having uniform linear charge density and passing through the axis of a cylinder is removed.
 AdecreaseBincreasesCremains sameDcannot say
AdecreaseBincreasesCremains sameDcannot sayA non conducting infinite rod is placed along the z−axis the upper half of the rod (lying along z≥0) is charged positively with a uniform linear charge density +λ, while the lower half (z<0) is charged negatively with a uniform linear charge density −λ. The origin is located at the junction of the positive and negative halves of the rod. A uniformly charged annular disc (surface charge density : σ0) of inner radius R and outer radius 2R is placed in the x−y plane with its centre at the origin. find the force on the rod due to the disc.
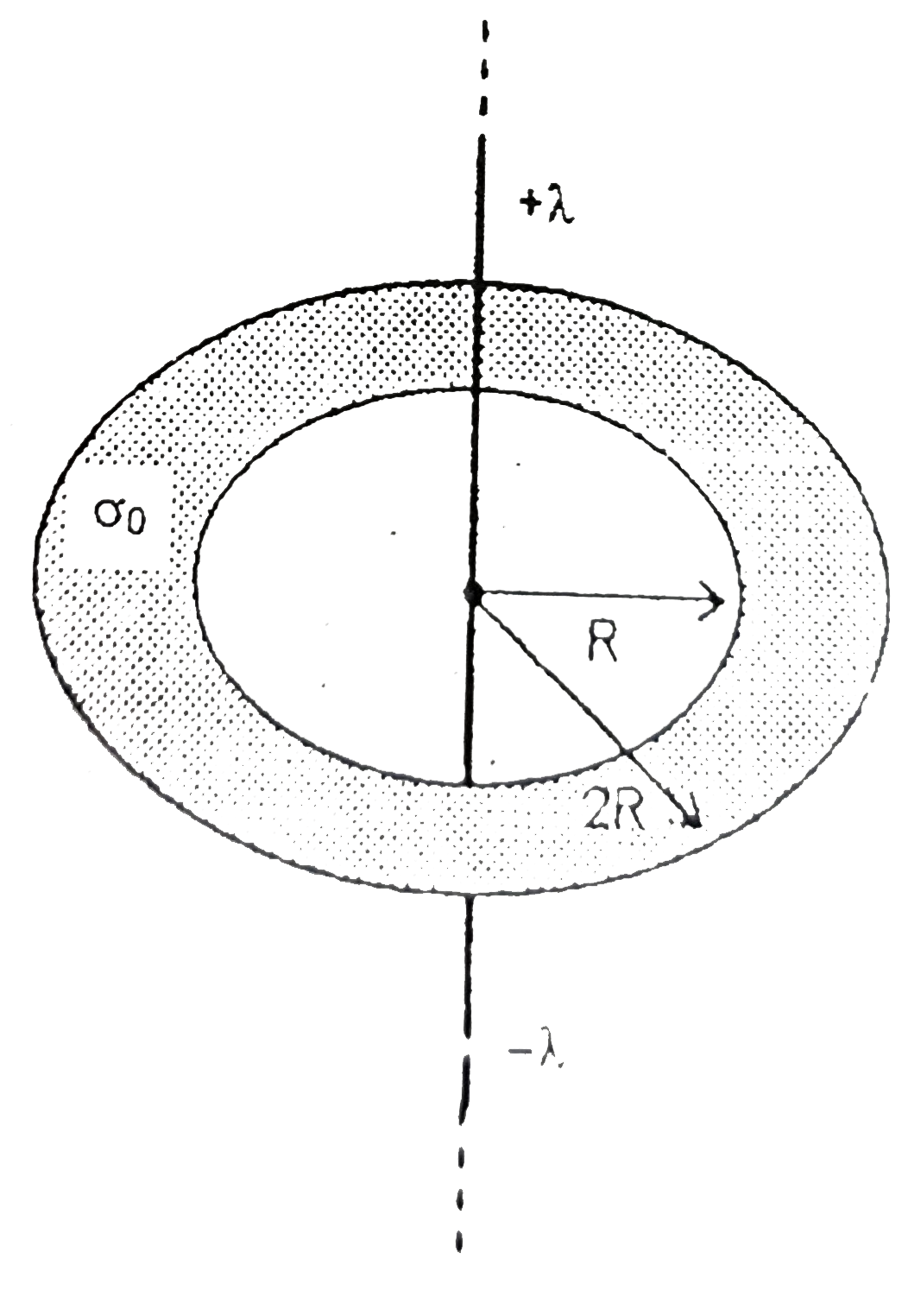 A2σ0λRε0Bσ0λR2ε0Cσ0λRε0Dσ0λR3ε0
A2σ0λRε0Bσ0λR2ε0Cσ0λRε0Dσ0λR3ε0
Three non-conducting infinite planar sheets are parallel to the y-z plane. Each sheet has an unifomi surface charge density. The first sheet, with a negative surface charge density σ, passes through the x-axis at x = Im. The second sheet has an unknown surface charge density and passes through the x- axis at x = 2m. The third sheet has a negative surface charge density-3cr and passes through the x-axis atx = 4m. The net electric field due to the sheets is zero at x = 1.5m. Which of the following is/are correct :
View SolutionFind the distance of the z-axis from the image of the point M(2−3,3) in the plane x−2y−z+1=0.
View SolutionThere is a plane of uniform positive charge density o parallel to the yz-plane and located at x = 2d. A point charge q+ is placed at the origin. Solve for the position x along the x-axis, where a positive test charge will have a net force of zero.

View SolutionFind ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
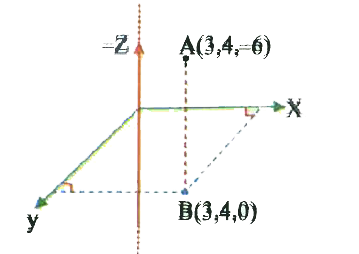
View SolutionIn a certain region of space, there exists a uniform and constant electric field of strength E along x-axis and uniform constant magnetic field of induction B along z-axis. A charge particle having charge q and mass m is projected with speed v parallel to x-axis from a point (a, b, 0). When the particle reaches a point 2a, b/2, 0 its speed becomes 2v. Find the value of electric field strength of m, v and co-ordinates.
View Solution
