एक धारावाही कुण्डली को दो एकसमान R त्रिज्या वाले अर्द्धवृत्तीय भागों को जोड़कर बनाया जाता है, जिसमें एक भाग xy तल के अनुदिश तथा अन्य दूसरा भाग X-Z तल के अनुदिश है। यदि कुण्डली में प्रवाहित धारा I हो तो दोनों अर्द्धवृत्तीय भाग के कारण, उनके द्वारा उभयनिष्ठ केन्द्र पर परिणामी चुम्बकीय क्षेत्र होगा
μ0I2√2R
μ0I2R
μ0I4R
μ0I√2R
The correct Answer is:A
प्रश्न में दिए गए लूप चित्र में दर्शाये अनुसार होंगे

x -y तल में स्थित अवृत्तवृत्ताकार लूप के कारण केंद्र पर चुम्बकीय क्षेत्र Bxy=12(μ0l2R), त्राणात्मक Z दिशा
इसी प्रकार x -z तल में लूप के कारण क्षेत्र Bxz=12(μ0l2R) त्राणात्मक y दिशा
∴ परिणामी चुम्बकीय क्षेत्र का परिमाण
B=√B2xy+B2xz=√(μ0i4R)2+(μ0l4R)2
=μ0i4R√2=μ0l2√2R प्रश्न में दिए गए लूप चित्र में दर्शाये अनुसार होंगे

x -y तल में स्थित अवृत्तवृत्ताकार लूप के कारण केंद्र पर चुम्बकीय क्षेत्र Bxy=12(μ0l2R), त्राणात्मक Z दिशा
इसी प्रकार x -z तल में लूप के कारण क्षेत्र Bxz=12(μ0l2R) त्राणात्मक y दिशा
∴ परिणामी चुम्बकीय क्षेत्र का परिमाण
B=√B2xy+B2xz=√(μ0i4R)2+(μ0l4R)2
=μ0i4R√2=μ0l2√2R
Topper's Solved these Questions
Similar Questions
m द्रव्यमान के तीन कण स्थिर घर्षणरहित क्षैतिज वृत्ताकार पथ पर समान क्षैतिज तल में चित्रानुसार फिसल सकते है। प्रत्यावस्थान गुणांक e= 0.5 है। यह मानिये कि m2 तथा m3 प्रारम्भ में विराम पर है तथा टक्कर के पहले त्रिज्यीय रेखा के अनुदिश स्थित है, तथा स्प्रिंग प्रारम्भ में मूल लम्बाई में है। तब अगली गति में स्प्रिंग में अधिकतम् विस्तार होगा।

View Solutionहम कैसे एक अनंत आवेशित रेखा के पास एक द्विध्रुव रख सकते हैं ताकि द्विध्रुव का कुल बल शून्य हो | चित्र द्वारा समझाइये |
View Solutionएक आयत की भुजाओं की लम्बाईयाँ a और b है। यदि उसके एक शीर्ष को मुलबिन्दु तथा x- अक्ष को भुजा a के अनुदिश ले तो आयत की भुजाओं के समीकरण ज्ञात कीजिए।
View Solutionसुसंगत क्षेत्र के बाहा भाग के किसी भी बिंदु को कहते है
View Solutionदिये गये चित्र में छायांकित भाग निम्न सुसंगत क्षेत्र को दर्शाता है -
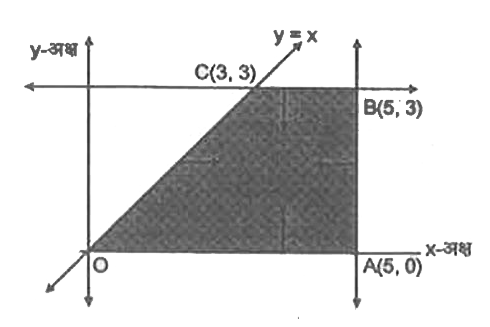
तो प्रतिबन्ध है -
View Solutionमाना एक दीर्घवृत्त जिसका दीर्घ -अक्ष, X-अक्ष के अनुदिश है तथा केन्द्र मूलबिंदु पर है, के नाभिलम्ब की लम्बाई 8 है । यदि दीर्घवृत्त की नाभियो के बीच की दुरी, इसके लघु-अक्ष की लम्बाई के समान हो, तो निम्न में से कौन-सा बिन्दु इस पर स्थित है?
View Solutionएक बिंदु p को एक वृत्त के भीतरी भाग से यादृच्छिक रूप से चयन किया जाता है, तो वह, प्रायिकता क्या होगी जिससे यह वस्तुतः वृत्त की परिसीमा के नजदीक होने की बजाय वृत्त के केंद्र से अधिक नजदीक होगा।
View Solutionकॉलम - I में कुछ निश्चित स्थितियां दी गई है जिनमे प्रतिरोध का सीधा धात्विक तार प्रयुक्त किया है तथा कॉलम - II में कुछ परिणामी प्रभाव दिए है कॉलम - I के कथनो को कॉलम - II के कथनो से सुलमित कीजिए
कॉलम - I कॉलम - II(A)एक आवेशित संधारित्र को तार के सिरों से जोड़ा गया है(p) एक नियत धारा तार में से प्रवाहित होती है(B)तार को इसकी लम्बाई के लम्बवत नियत वेग से एक समान चुम्बकीय क्षेत्र में गतिमान किया जाता है चुम्बकीय क्षेत्र गति के तल के लम्बवत है(q)उष्मीय ऊर्जा तार में उत्पन्न होती है(C)तार को नियत विधुत क्षेत्र में रखा जाता है जिसकी दिशा तार की लम्बाई के अनुदिश है(r)तार के सिरों पर एक नियत विभवान्तर उत्पन्न होता है(D)तार के सिरों पर एक नियत वि. वा. बल. की बैट्री जोड़ी जाती है(s)तार के सिरों का नियत परिमाण का आवेश उपस्थित होता है
View Solutionआयत के भाग के रूप में त्रिभुज |आयत के अन्य भाग
View Solutionलम्बी धारावाही परिनालिका के कारण चुम्बकीय क्षेत्र|टोरॉइड #!#टोरोइड के कारण चुम्बकीय क्षेत्र
View Solutionलम्बी धारावाही परिनालिका के कारण चुम्बकीय क्षेत्र|टोरॉइड #!#टोरोइड के कारण चुम्बकीय क्षेत्र
View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solutionयदि 5m तार को 8 भागों में विभाजित करते है तो हर एक भाग की लम्बाई ज्ञात करो।
View Solutionएक 713 मीटर लम्बे तार को 7 बराबर भागों में काटा जाता है तब प्रत्येक भाग की लम्बाई होगी
View Solutionजब विद्युत धारा को अम्लीय जल के माध्यम से प्रवाहित किया जाता है, तो NTP पर 112 mL हाइड्रोजन गैस 965 सेकंड में कैथोड पर एकत्र हो जाती है। एम्पियर में प्रवाहित धारा है:
View Solutionएक क्रिस्टलीय ठोस X, Y और Z से बना है। घनीय निविड संकुलित (ccp) जालक में X के परमाणु उपस्थित हैं, Y सभी अष्टफलकीय रिक्तियों को ग्रहण करता है और Z सभी चतुष्फलकीय रिक्तियों को ग्रहण करता है। यदि एक काय विकर्ण के अनुदिश सभी परमाणुओं को हटा दिया जाता है, तो ठोस का सूत्र होगा :
View Solution
