Find the equation of circles determined by the following conditions. The centre at (3, 2) and circle is tangent to x-axis.Solution in Odia
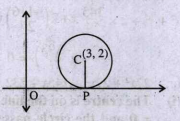 ∴ Radius = 2
∴ Radius = 2
∴ Eqn. of the circle is
(x−h)2+(y−k)2=a2
or, (x−3)2+(y−2)2=4
or, x2+9−6x+y2+4−4y=4
x2+y2−6x−4y+9=0
Topper's Solved these Questions
Similar Questions
Multiply (2√−3+3√−2) by (4√−3−5√−2)
View SolutionFind the points where the following function are not differentiable.
e|x|
View SolutionFind the equation of the circle touching : x-axis andhaving centre at (4, 3)
View SolutionA circle of radius 2 units rools on the outer side of the circle x2+y2+4x=0, touching it externally. Find the locus of the centre of this outer circle. Also find the equations of the common tangents of the two circles when the line joining the centres of the two circles makes an angle of 600 with x-axis.
View SolutionA circle passes through the points (-3, 4), (1, 0) and its centre lies on the x-axis. Find the equation of the circle.
View SolutionFind the equation of the circle having
centre at (7,-2) , and touching the X-axis
View SolutionEquation of of circle centred at (-4, 3) , and tangent to Y-axis , is
View SolutionFind the equation of circles determined by the following conditions. The centre at (1, 4) and passing through (-2, 1).
View SolutionFind the equation of circles determined by the following conditions. The centre at (-1, 4) and circle tangent to y-axis.
View SolutionFind the equation of circles determined by the following conditions. The radius is 5 and circle is tangent to both axes.
View SolutionFind the equation of circles determined by the following conditions.The centre is on the x-axes and the circle passes through the origin and the point (4, 2).
View SolutionFind the equation of circles determined by the following conditions. The centre is on the line 8x+5y=0 and the circle passes through the points (2, 1) and (3, 5).
View SolutionFind the equation of circles determined by the following conditions. The centre is on the line 2x+y-3=0 and the circle passes through the points (5, 1) and (2, -3).
View SolutionFind the equation of circles determined by the following conditions. The circle touches the axis of x at (3, 0) and also touches the line 3y - 4x =12.
View SolutionFind the equation of circles determined by the following conditions. Circle is tangent to x-axis and passes through (1, -2) and (3, -4)
View Solution
