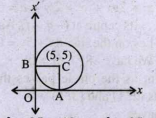
Find the equation of circles determined by the following conditions. The radius is 5 and circle is tangent to both axes.Solution in Odia
As the circle is tangent to both the axes, we have its centre at (5, 5).
∴ Equation of the circle is
or, (x±5)2+(y±5)2=25
 or, x2+25±10x+y2+25±10y=25
or, x2+25±10x+y2+25±10y=25
or, x2+y2±10x±10y+25=0
Topper's Solved these Questions
Similar Questions
Multiply (2√−3+3√−2) by (4√−3−5√−2)
View SolutionFind the points where the following function are not differentiable.
e|x|
View SolutionA circle touches both the axes and its centre lies in the fourth quadrant.If its radius is 1 then find the equation of circle.
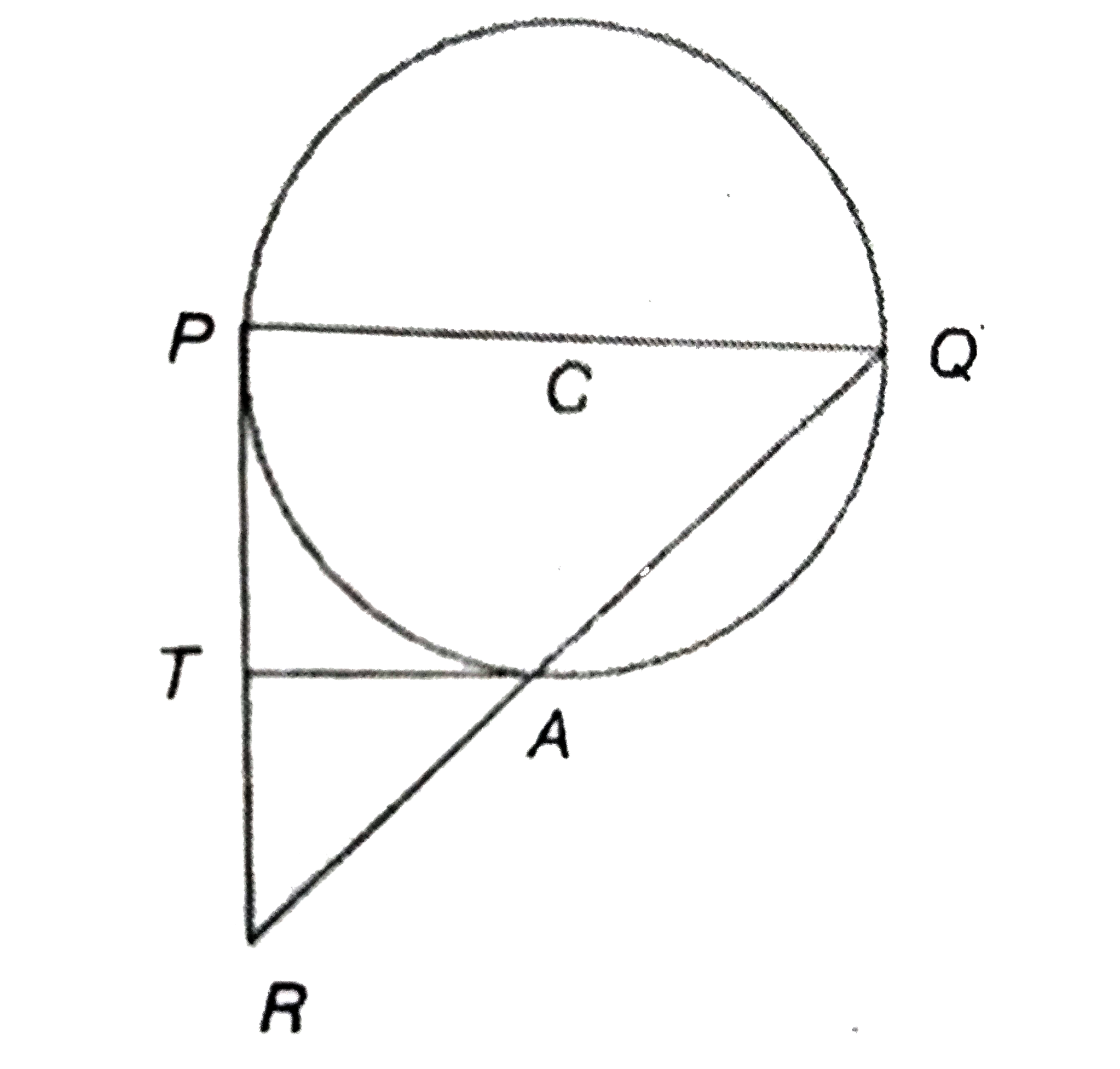
View SolutionIn the following figure,PQ is the diameter of the circle with radius 5 cm. if AT is the tangent and equal to the radius of the circle, then find the lenth of AR.
View Solution3 त्रिज्या वाले दोनों अक्षो को स्पर्श करते हुए वृत्त का समीकरण निकाले।
View Solutionउस वृत्त का समीकरण निकालिए जो दोनों अक्षों को स्पर्श करता है तथा जिसकी त्रिज्या a है।
View Solutionत्रिज्या r का वृत्त द्वितीय चतुर्थाश में स्थित है । यदि वृत्त दोनों अक्षों को स्पर्श करता है तो वृत्त का समीकरण ज्ञात कीजिए ।
View SolutionEquation of the circle of radius 5 which touches both the coordinate axes is
View SolutionA circle of radius 3 units touches both the axes. Find the equations of all possible circles formed in the general form.
View SolutionThe equation of a circle of radius r and touching both the axes is
View Solutionएक वृत्त की त्रिज्या a है और यह प्रथम चतुर्थाश में दोनों अक्षों को स्पर्श करता है, वृत्त का समीकरण ज्ञात कीजिए |
View SolutionCircle touching both the axes and radius 5 is
View SolutionThe radius of a circle is a and it touches both axes in the first quadrant, find the equation of the circle.
View SolutionFind the equation of circles determined by the following conditions. The centre at (3, 2) and circle is tangent to x-axis.
View SolutionFind the equation of circles determined by the following conditions. The centre at (-1, 4) and circle tangent to y-axis.
View Solution
