Find the length of the tangent, drawn to the circles x2+y2+10x−6y+8=0 from the centre of the circle x2+y2−4x=0Solution in Odia
Centre of the circle
x2+y2−4x=0 is (2, 0).
∴ Length of the tangent drawn from the point (2, 0) to the circle
x2+y2+10x−6y+8=0 is
√x21+y21+2gx1+2fy1+c
= √4+0+10×2+0+8=√32=4√2
Topper's Solved these Questions
Similar Questions
Multiply (2√−3+3√−2) by (4√−3−5√−2)
View SolutionFind the points where the following function are not differentiable.
e|x|
View SolutionCombined equation to the pair of tangents drawn from the origin to the circle x^(2)+y^(2)+4x+6y+9=0 is
View SolutionThe number of common tangents to the circles x2+y2−4x+6y+8=0andx2+y2−10x−6y+14=0 is : (A) 2 (B) 3 (C) 4 (D) none of these
View SolutionTangents are drawn from a point on the circle x2+y2−4x+6y−37=0 to the circle x2+y2−4x+6y−12=0. The angle between the tangents, is
View SolutionFind the equations of the tangents from the point A(3,2) to the circle x2+y2+4x+6y+8=0.
View SolutionThe number of common tangents that can be drawn to the circles x2+y2−4x+6y+8=0,x2+y2−10x−6y+14=0
View SolutionThe length of the tangent from a point on the circle x2+y2+4x−6y−12=0 to the circle x2+y2+4x−6y+4=0 is
View SolutionThe number of tangents that can be drawn from (6,0) to the circle x2+y2−4x−6y−12=0 are
View SolutionFind the length of the tangent from any point on the circule
x2+y2−4x+6y−2=0 to the circle x2+y2−4x+6y+7=0
View Solutionস্পর্শকের দৈর্ঘ্য নির্ণয় করো:
x2+y2−4x+6y−2=0 বৃত্তের ওপর যে-কোনো বিন্দু থেকে x2+y2−4x+6y+7=0 বৃত্তে অঙ্কিত স্পর্শকের দৈর্ঘ্য নির্ণয় করো
View Solution(−3,9) বিন্দু থেকে x2+y2−4x+6y−12=0 বৃত্তে অঙ্কিত স্পর্শকের দৈর্ঘ্য নির্ণয় কর।
View SolutionThe length of the tangent drawn from any point on the circle : x2+y2−4x+2y−4=0 to the circle x2+y2−4x+6y=0 is :
View Solution(i) Find the equation of the tangents to the circle x2+y2−4x+6y−12=0 which are parallel to x+y−8=0
(ii) Find the equations of the tangents to the circle x2+y2−5x+6y−12=0 which are paralel to x+2y−8=0
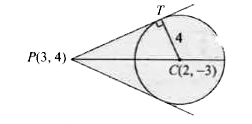
View SolutionFind the length of a tangent drawn from the point (3,4) to the circle x2+y2−4x+6y−3=0.
View Solution
