In the experiment of Ohm's law, when potential difference of 10.0 V is applied, current measured is 1.00 A. If length of wire is found to be 10.0cm and diameter of wire 2.50 mm, then find maximum permissible percentage error in resistivity.
The correct Answer is:C
R=ρlA=VI
where,(ρ)= resistivity and
A= cross sectional area
Therefore. from Eq. (i)
ρ=AVlI=πd2V4lI
Where, A=πd24
From Eq. (ii) we can see that maximum permissible percentage error in (rho) will be
Δρρ×100=[2(Δdd)+(ΔVV)+(Δll)+(ΔII)]×100
=[2×0.012.50+0.110.0+0.110.0+0.011.00]×100
=3.8%.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.12videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.22videos
EXPERIMENTS
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer17videos
ELECTROSTATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
Similar Questions
If the least count of a screw gauge is 0.001 cm and diameter of a wire measured by it is 0.236 cm, find the permissible percentage error in the measurement.
View SolutionIn ohm's law experiment potential drop across a resistance was measured as v=5.0 volt and current was measured as I=2.0amp If least count of the volmeter and ammeter are 0.1V and 0.01A respectively then find the maximum permissible error in resistance .
View SolutionIn an experiment, current measured is, I=10.0A, potential difference measured is V=100.0V, length of the wire is 31.4cm and the diameter of the wire 2.00mm (all in correct significant figures). Find resistivity of the wire in correct significant figures. [Take π=3.14, exact].
(a)
(b)
(c)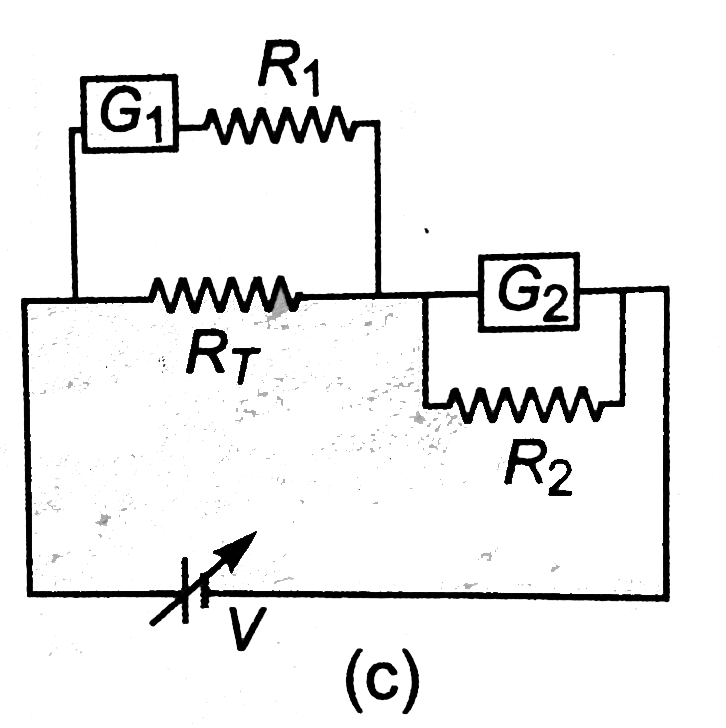
(d)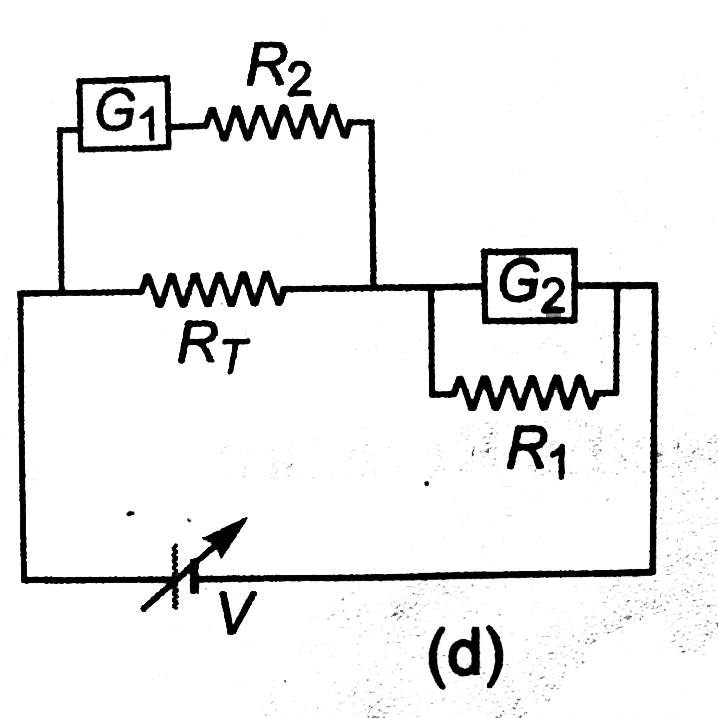
.View SolutionIn u−v method to find focal length of a concave mirror, if object distance is found to be 10.0cm and image distance was also found to be 10.0cm, then find maximum permissible error in (f).
View SolutionIn Searle's exp to find Young's modulus, the diameter of wire is mesured as D=0.05cm length of wire is L=125cm, and when a weight, m=20.0kg is put, extension in wire was found to be 0.100cm. Find maximum permissible percentage error in Young's modulus (Y)
View SolutionIf the measured value of resistance R=1.05Ω, wire diameter d=0.60mm , and length l=75.3cm, then find the maximum permissible error in resistivity ,
ρ=R(πd2/4)l.View SolutionFrom some instruments current measured is I=10.0amp, potential different measured is V=100.0V, length of wire is 31.4cm, and diameter of wire is 2.00mm (all in correct significant figure). The resistivity of wire (in correct significant figures)will be (use π=3.14)
View SolutionWhen a potential difference of 3 V is applied between the two ends of a 60 cm long metallic wire, current density in it is found 10 be 1×10−7Am−2 Find conductivity of the material of the wire in SI system.
View SolutionIn Ohm's law experiment , the potential drop acros a resistance was as V=5.0V and the current was measured as I=2.00A. Find the maximum permissible error in resistance.
View SolutionA current of 0.2 A flows through a wire whose ends are at a potential difference of 15 V. Calculate :
the resistance of the wire,View Solution