From some instruments current measured is , potential different measured is , length of wire is , and diameter of wire is (all in correct significant figure). The resistivity of wire (in correct significant figures)will be (use )
The correct Answer is:A
To find the resistivity of the wire, we will follow these steps:
Step 1: Calculate the Resistance (R)
Using Ohm's Law, the resistance R can be calculated using the formula:
R=VI
Where:
- V=100.0V
- I=10.0A
Substituting the values:
R=100.0V10.0A=10.0Ω
Step 2: Convert Length to Meters
The length of the wire is given as 31.4cm. We need to convert this to meters:
L=31.4cm=31.4×10−2m=0.314m
Step 3: Calculate the Cross-sectional Area (A)
The diameter of the wire is given as 2.00mm. We need to convert this to meters:
d=2.00mm=2.00×10−3m
The area A of the wire can be calculated using the formula for the area of a circle:
A=πd24
Substituting π=3.14 and d=2.00×10−3m:
A=3.14×(2.00×10−3)24
Calculating (2.00×10−3)2:
(2.00×10−3)2=4.00×10−6
Now substituting back into the area formula:
A=3.14×4.00×10−64=3.14×10−6m2
Step 4: Calculate the Resistivity (ρ)
Using the formula for resistivity:
ρ=R⋅AL
Substituting the values we have:
ρ=10.0Ω⋅3.14×10−6m20.314m
Calculating 3.14×10−60.314:
3.14×10−60.314=1.00×10−5
Now substituting this back into the resistivity formula:
ρ=10.0⋅1.00×10−5=1.00×10−4Ω⋅m
Final Answer
The resistivity of the wire is:
ρ=1.00×10−4Ω⋅m
Using Ohm's Law, the resistance R can be calculated using the formula:
R=VI
Where:
- V=100.0V
- I=10.0A
R=100.0V10.0A=10.0Ω
The length of the wire is given as 31.4cm. We need to convert this to meters:
L=31.4cm=31.4×10−2m=0.314m
The diameter of the wire is given as 2.00mm. We need to convert this to meters:
d=2.00mm=2.00×10−3m
The area A of the wire can be calculated using the formula for the area of a circle:
A=πd24
Substituting π=3.14 and d=2.00×10−3m:
A=3.14×(2.00×10−3)24
Calculating (2.00×10−3)2:
(2.00×10−3)2=4.00×10−6
Now substituting back into the area formula:
A=3.14×4.00×10−64=3.14×10−6m2
Using the formula for resistivity:
ρ=R⋅AL
Substituting the values we have:
ρ=10.0Ω⋅3.14×10−6m20.314m
Calculating 3.14×10−60.314:
3.14×10−60.314=1.00×10−5
Now substituting this back into the resistivity formula:
ρ=10.0⋅1.00×10−5=1.00×10−4Ω⋅m
The resistivity of the wire is:
ρ=1.00×10−4Ω⋅m
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MCQ_TYPE17videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - MATCH THE COLUMN6videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery49videos
FLUID MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
Similar Questions
In an experiment, current measured is, I=10.0A, potential difference measured is V=100.0V, length of the wire is 31.4cm and the diameter of the wire 2.00mm (all in correct significant figures). Find resistivity of the wire in correct significant figures. [Take π=3.14, exact].
(a)
(b)
(c)
(d)
.View SolutionRadius of a wire is 2.50 mm. The length of the wire is 50.0 cm. If mass of wire was measured as 25g, then find the density of wire in correct significant figures.
[Given,π=3.14,exact]View SolutionA thin wire has a length of 21.7 cm and radius 0.46 mm. Calculate the volume of the wire to correct significant figures.
View SolutionA thin wire has length of 21.7 cm and radius 0.46 mm. Calculate the volume of the wire to correct significant figures?
View SolutionA thin wire has length of 21.7 cm and radius 0.46 mm. Calculate the volume of the wire to correct significant figures?
View SolutionIn the experiment of Ohm's law, when potential difference of 10.0 V is applied, current measured is 1.00 A. If length of wire is found to be 10.0cm and diameter of wire 2.50 mm, then find maximum permissible percentage error in resistivity.
View SolutionIf the length of wire is (100.0 cm) and radius of wire as measured from screw gauge is (1.00mm) then the specific resistance of wire material is .
View SolutionThe diameter of a wire is measured to be 0.0250 × 10−4 m. The number of significant figures in the measurement is
View SolutionIf resistance S in RB=300Ω, then the balanced length is found to be 25.0cm from end A. The diameter of unknown wire is 1mm and length of the unknown wire is 3.14cm. The specific resistivity of the wire should be
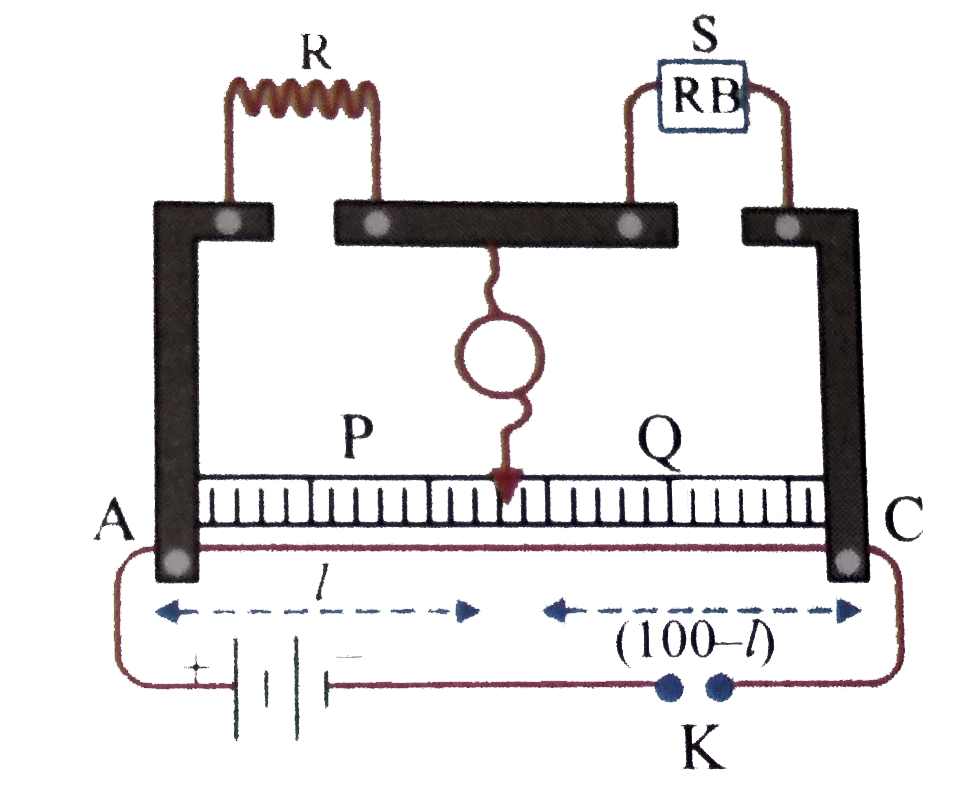View SolutionWhen 115V is applied across a wire that is 10m long and has a 0.30mm radius, the current density is 1.4×104A/m2. The resistivity of the wire is
View Solution