For positive error, the correction is.
Positive
negative
nil
may be positive or negative
The correct Answer is:B
To solve the question "For positive error, the correction is," we can follow these steps:
1. Understand the Concept of Error:
- In measurements, an error can be classified as positive or negative. A positive error indicates that the measured value is greater than the actual value.
2. Define the Variables:
- Let the actual value of the quantity be represented as x.
- Let the error be represented as Δx.
3. Express the Measured Value:
- If there is a positive error, the measured value can be expressed as:
Measured Value=x+Δx
- Here, x+Δx is greater than x because Δx is positive.
4. Determine the Correction Needed:
- To find the actual value x from the measured value x+Δx, we need to correct the measured value by removing the error.
- This means we need to subtract Δx from the measured value:
Correction=x+Δx−Δx=x
- Therefore, the correction needed is:
Correction=−Δx
5. Conclusion:
- Since we are subtracting Δx to correct the positive error, the correction is negative. Thus, the answer to the question is that the correction for a positive error is negative.
Final Answer:
- The correction for a positive error is negative.
---
- In measurements, an error can be classified as positive or negative. A positive error indicates that the measured value is greater than the actual value.
- Let the actual value of the quantity be represented as x.
- Let the error be represented as Δx.
- If there is a positive error, the measured value can be expressed as:
Measured Value=x+Δx
- Here, x+Δx is greater than x because Δx is positive.
- To find the actual value x from the measured value x+Δx, we need to correct the measured value by removing the error.
- This means we need to subtract Δx from the measured value:
Correction=x+Δx−Δx=x
- Therefore, the correction needed is:
Correction=−Δx
- Since we are subtracting Δx to correct the positive error, the correction is negative. Thus, the answer to the question is that the correction for a positive error is negative.
- The correction for a positive error is negative.
Topper's Solved these Questions
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Subjective
15 Videos
- EXPERIMENTSBOOK - DC PANDEY ENGLISHCHAPTER - EXPERIMENTSEXERCISE - Exercise 3.8
3 Videos
- ELECTROSTATICSBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Integer
17 Videos
- FLUID MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - Medical entranes gallery
49 Videos
Similar Questions
Knowledge Check
A pendulum is oscillaring on either side its rest position.The correct statement is:
AIt has the maximum potential energy at its extreme position.BIt has the maximum kinetic energy at its extreme position.Cit has the maximum potential energy at its mean position.DThe sum of its kinetic and potential energies remains constant throughout the motion.While measuring the acceleration due to gravity by a simple pendulum, a student makes a positive error of 1% in the length of the pendulum and a negative error of 3% in the value and a of time period. His percentage error in the measurement of g by the relation g=4π2(l/T2) will be
AA) 0.02BB) 0.04CC) 0.07DD) 0.1
In an experiment of determine acceleration due to gravity by simple pendulum, a student commits 1% positive error in the measurement of length and 3% negative error in the time then % error in g will be
View SolutionIn the compound given below
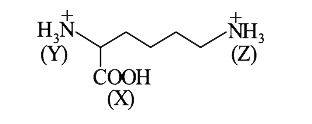
the correct order of actidity of positions X,Y,Z is
View SolutionIf there is a positive error of 50% in the measurement of velocity of a body , find the error in the measurement of kinetic energy.
View SolutionWhile measuring acceleration due to gravity by a simple pendulum , a student makes a positive error of 2% in the length of the pendulum and a positive error of 1% in the measurement of the value of g will be
View SolutionAssertion : Absolute error may be negative or positive.
Reason : Absolute error is the difference between the real value and the measured value of a physical quantity.
View SolutionPick out the error and write correct IUPAC name of pent-3-yne.
View Solution
