Two resistances are connected in the two gaps of a meter bridge. The balance point is 20cm from the zero end. When a resistance 15Ω is connected in series with the smaller of two resistance, the null point+ shifts to 40cm. The smaller of the two resistance has the value.
3
6
9
12
The correct Answer is:C
To solve the problem step by step, we will use the principles of a meter bridge and the concept of balancing the circuit.
Step 1: Understand the Setup
We have two resistances, let's denote them as:
- R1=X (the smaller resistance)
- R2=Y (the larger resistance)
The balance point is initially at 20 cm from the zero end of the meter bridge.
Step 2: Apply the Balance Condition
According to the meter bridge principle, when the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths from the zero end:
X20=Y80
This can be rearranged to give:
X=Y4(Equation 1)
Step 3: Introduce the Additional Resistance
Now, when a resistance of 15Ω is connected in series with the smaller resistance X, the new balance point shifts to 40 cm.
Step 4: Apply the Balance Condition Again
Using the new balance point, we can write:
X+1540=Y60
Rearranging gives:
X+15=2Y3(Equation 2)
Step 5: Substitute Equation 1 into Equation 2
Now we substitute X=Y4 from Equation 1 into Equation 2:
Y4+15=2Y3
Step 6: Solve for Y
To eliminate the fractions, multiply the entire equation by 12 (the least common multiple of 4 and 3):
12(Y4)+12×15=12(2Y3)
This simplifies to:
3Y+180=8Y
Rearranging gives:
180=8Y−3Y
180=5Y
Thus, we find:
Y=1805=36Ω
Step 7: Find X
Now, we can find X using Equation 1:
X=Y4=364=9Ω
Final Answer
The smaller of the two resistances X is 9Ω.
---
We have two resistances, let's denote them as:
- R1=X (the smaller resistance)
- R2=Y (the larger resistance)
According to the meter bridge principle, when the bridge is balanced, the ratio of the resistances is equal to the ratio of the lengths from the zero end:
X20=Y80
This can be rearranged to give:
X=Y4(Equation 1)
Now, when a resistance of 15Ω is connected in series with the smaller resistance X, the new balance point shifts to 40 cm.
Using the new balance point, we can write:
X+1540=Y60
Rearranging gives:
X+15=2Y3(Equation 2)
Now we substitute X=Y4 from Equation 1 into Equation 2:
Y4+15=2Y3
To eliminate the fractions, multiply the entire equation by 12 (the least common multiple of 4 and 3):
12(Y4)+12×15=12(2Y3)
This simplifies to:
3Y+180=8Y
Rearranging gives:
180=8Y−3Y
180=5Y
Thus, we find:
Y=1805=36Ω
Now, we can find X using Equation 1:
X=Y4=364=9Ω
The smaller of the two resistances X is 9Ω.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - B. Assertion and reason
18 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Match the columns
4 Videos
- CURRENT ELECTRICITYBOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Check point
70 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Subjective
11 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Medical entrances gallery
25 Videos
Similar Questions
Two resistances are connected in two gaps of a meter bridge. The balance point is 20cm from the zero end. A resistance of 15Ω is connected in series with the smaller of the two. The null point shifts to 40cm. The value of the smaller resistance in Ω is
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View SolutionWith two resistance R1andR2(>R1) in the two gaps of a metre bridge the balance was found to be 1/3 m from the zero end. When a 6Ωresistance is connected in series with the smaller of the two resistance, the point is shifted to 2/3 m from the same end, then R1andR2 are
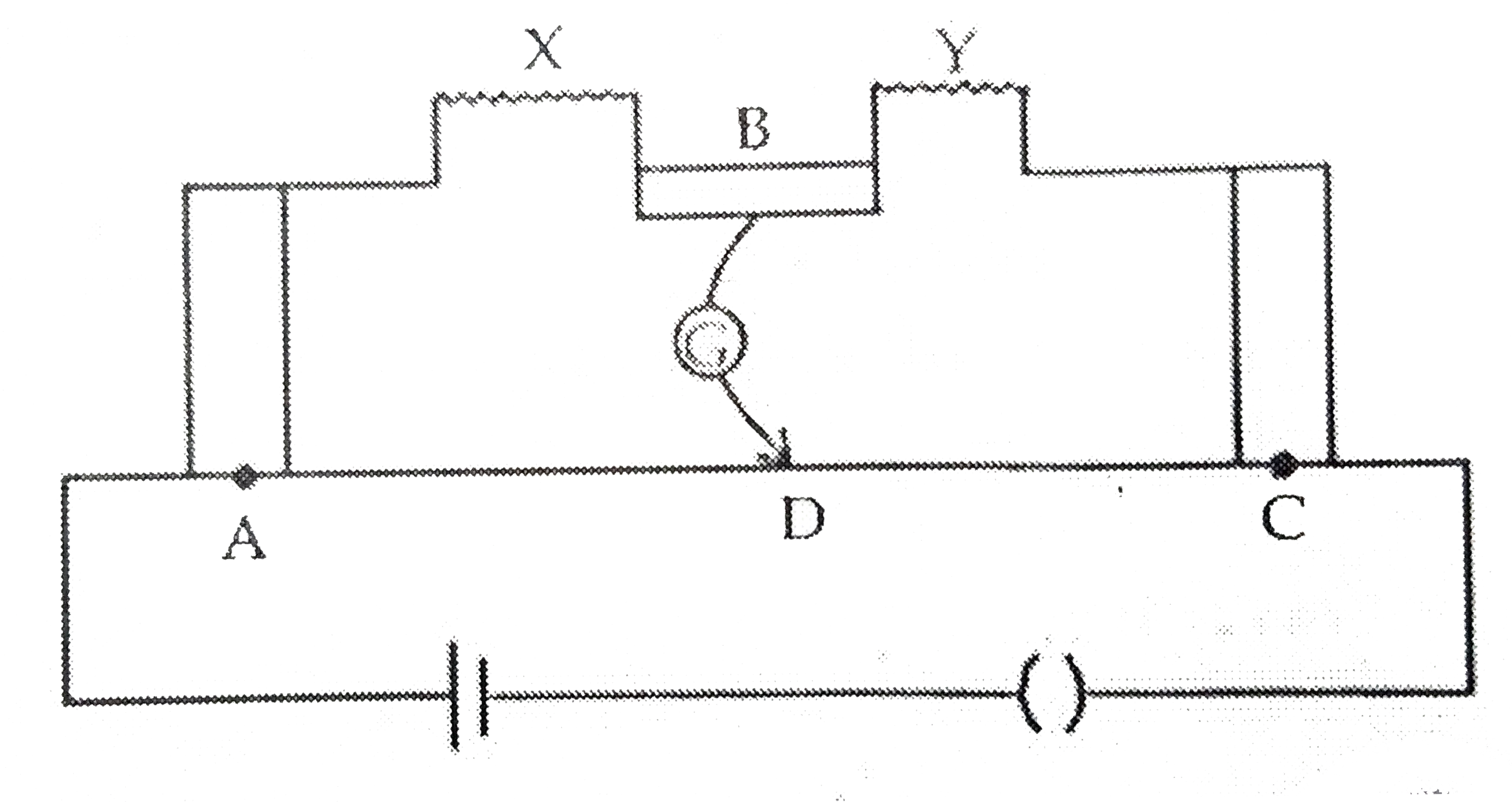
View SolutionThe figure shows experimental set up of a meter bridge. When the two unknown resistances X and Y are inserted, the null point D is obtained 40 cm from the end A. When a resistance of 10Ω is connected in series with X, the null point shifts by 10 cm. Find the position of the null point when the 10Ω resistance is instead connected in series with resistance 'Y'. Determine the value of the resistance X and Y
View SolutionTwo unkonwn resistances X and Y are connected to left and right gaps of a meter bridge and the balancing point is obtained at 80cm from left. When a 10Ω resistance is connected parallel to X, the balancing point is 50cm from left. The values of X and Y respectively are
View SolutionThe figure
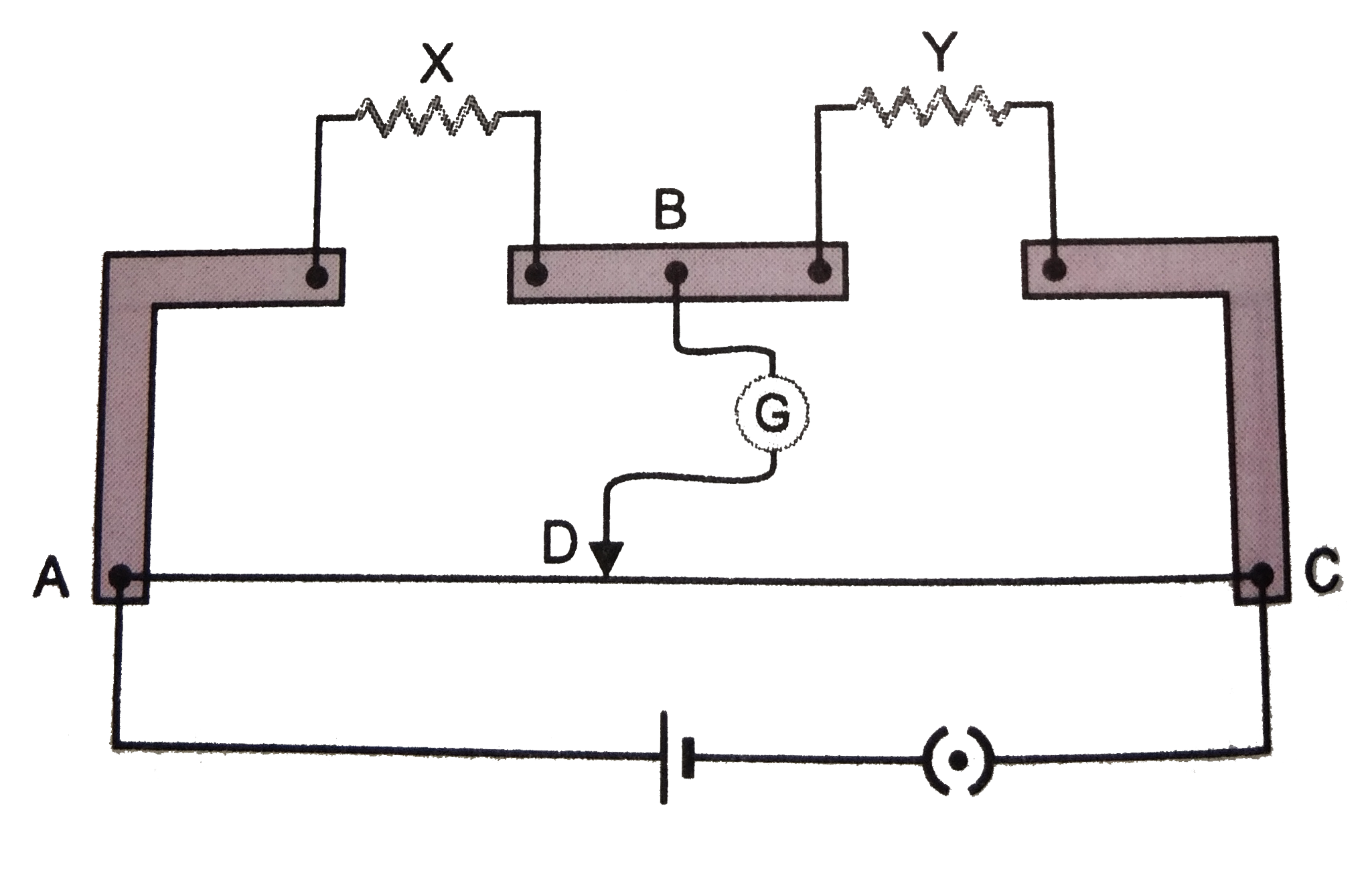
Shows the experimental set up of a meter bridge. The null point is found to be 60 cm away from the end A with X and Y in positions as shown. When a resistance of 15Ω is connected in series with Y, the null points is found to shift by 10 cm towards the end A of the wire. Find the position of the null point if resistance of 30Ω were connected in parallel with Y.
View SolutionThe resistance in the left and right gaps of a balanced meter bridge are R1 and R1. The balanced point is 50cm. If a resistance of 24Ω is connected in parallel to R2, the balance point is 70cm. The value of R1 or R2 is.
View SolutionIn a meter bridge, the null point is found at a distance of 40 cm from A. If now a resistance of 12 Ω is connected in parallel with S, the null point occurs at 60 cm from A. Determine the value of R.

View SolutionIn a meter bridge,
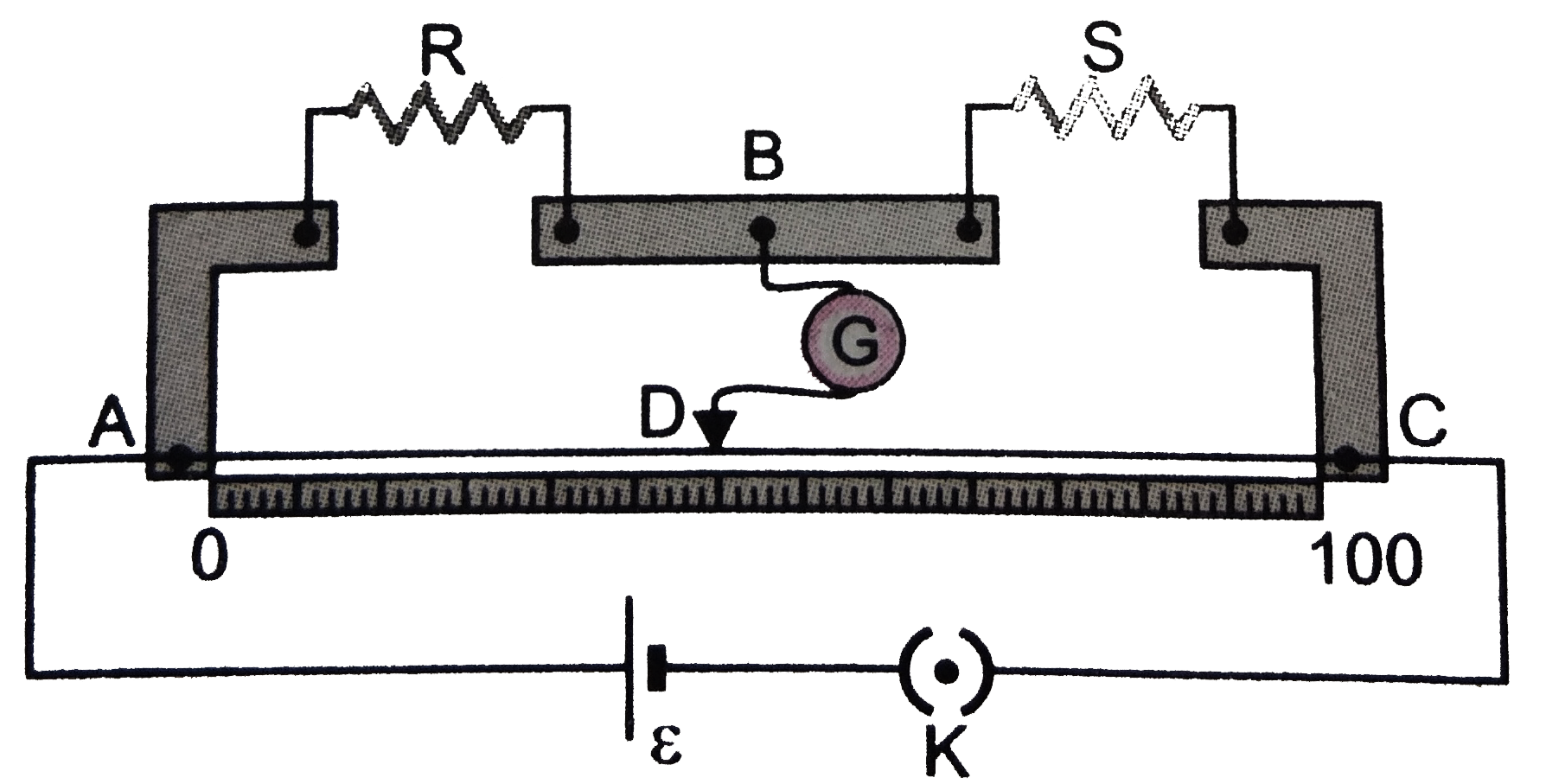
the null points is found at a distance of 33.7 cm from A. If now a resistance of 12Ω is connected in parallel with S, the null point occurs at 51.9 cm. Determine the values of R and S.
View SolutionWhen a resistance of 100Ω is connected in series with a galvanometer of resistance R, then its range is V. To double its range, a resistance of 1000Ω is connected in series. Find the value of R.
View Solution
