Resolve a weight of 10N in two directions which are parallel and perpendiular to a slope inclined at 30∘ to the horizontal.
To resolve a weight of 10 N in two directions that are parallel and perpendicular to a slope inclined at 30° to the horizontal, we can follow these steps:
Step 1: Understand the Problem
We have a weight (W) of 10 N acting vertically downwards. We need to resolve this weight into two components: one that is parallel to the slope and one that is perpendicular to the slope.
Step 2: Draw a Diagram
Draw a right triangle where:
- The vertical side represents the weight (10 N).
- The incline (slope) makes an angle of 30° with the horizontal.
- The angle between the weight and the perpendicular to the slope is also 30°.
Step 3: Identify the Angles
Since the slope is inclined at 30° to the horizontal, the angle between the weight and the slope is:
- 90° - 30° = 60° (for the parallel component)
- 30° (for the perpendicular component)
Step 4: Calculate the Perpendicular Component
The component of the weight acting perpendicular to the slope can be calculated using the cosine function:
W_{\perpendicular} = W \cdot \cos(30°)
Substituting the values:
W_{\perpendicular} = 10 \cdot \cos(30°)
W_{\perpendicular} = 10 \cdot \frac{\sqrt{3}}{2}
W_{\perpendicular} = 5\sqrt{3} \text{ N}
Step 5: Calculate the Parallel Component
The component of the weight acting parallel to the slope can be calculated using the sine function:
W∥=W⋅sin(30°)
Substituting the values:
W∥=10⋅sin(30°)
W∥=10⋅12
W∥=5 N
Final Result
- The component of the weight acting perpendicular to the slope is 5√3 N.
- The component of the weight acting parallel to the slope is 5 N.
We have a weight (W) of 10 N acting vertically downwards. We need to resolve this weight into two components: one that is parallel to the slope and one that is perpendicular to the slope.
Draw a right triangle where:
- The vertical side represents the weight (10 N).
- The incline (slope) makes an angle of 30° with the horizontal.
- The angle between the weight and the perpendicular to the slope is also 30°.
Since the slope is inclined at 30° to the horizontal, the angle between the weight and the slope is:
- 90° - 30° = 60° (for the parallel component)
- 30° (for the perpendicular component)
The component of the weight acting perpendicular to the slope can be calculated using the cosine function:
W_{\perpendicular} = W \cdot \cos(30°)
Substituting the values:
W_{\perpendicular} = 10 \cdot \cos(30°)
W_{\perpendicular} = 10 \cdot \frac{\sqrt{3}}{2}
W_{\perpendicular} = 5\sqrt{3} \text{ N}
The component of the weight acting parallel to the slope can be calculated using the sine function:
W∥=W⋅sin(30°)
Substituting the values:
W∥=10⋅sin(30°)
W∥=10⋅12
W∥=5 N
- The component of the weight acting perpendicular to the slope is 5√3 N.
- The component of the weight acting parallel to the slope is 5 N.
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 5.1
5 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 5.2
4 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
Resolve a weight of 10 N in two directions which are parallel and perpendicular to a slope inclined at 30∘ to the horizontal.
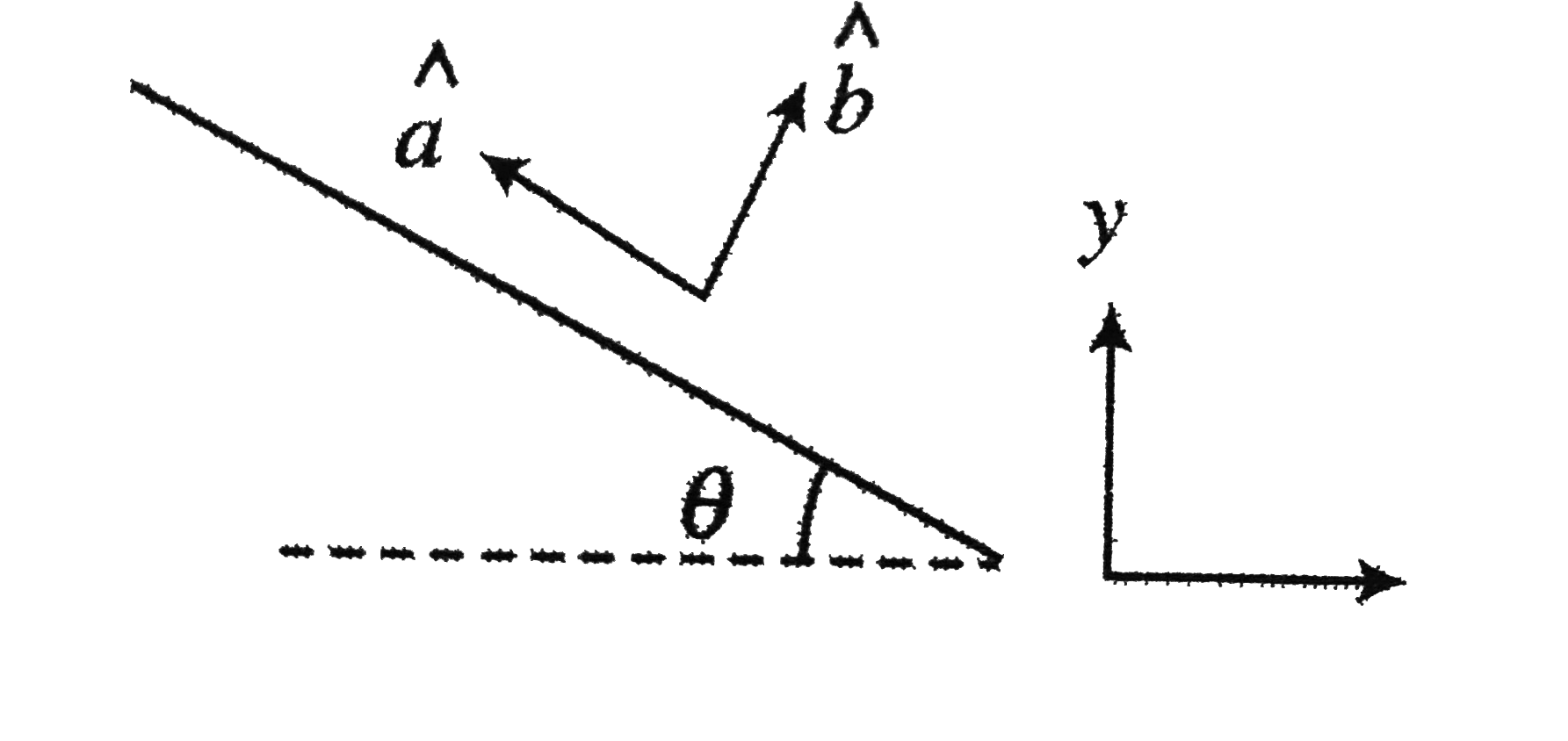
View SolutionAn inclined plane is inclined at θ with horizontal as shown in (figure).Write a unit vector in the direction parallel (ˆa) and perpendicular (ˆb) to inclined plane,in standard xy coordinate system.
View SolutionFind the slope of a line whose inclination is
30∘
View SolutionA block of weight 100 N is slowly slide up on a smooth incline of inclination 370 by as person. Calculate the work done by the person in moving the block through a distance of 2.0 m, if the driving force is a. parallel to the incline and b. in the horizontal direction.
View SolutionA block of weight 100 N is slowly slid up on a smooth incline of inclination 370 by as person. Calculate the work done by the person in moving the block through a distance of 2.0 m, if the driving force is a. parallel to the incline and b. in the horizontal direction.
View SolutionThe direction of motion of a projectile at a certain instant is inclined at an angle 60∘ to the horizontal. After √3 seconds it is inclined an angle 30∘. If the horizontal compound of velocity of projection is 3n (in m/sec) then value of n is : (takeg=10m/s2)
View SolutionAssertion: A body of weight 10N (W) is at rest on an inclined plane (μ=√32) making an angle of 30∘ with the horizontal. The force of friction acting on it is 5N
Reason: In above situation, the limiting force of friction is given by flimitting=μWcosθ=7.5N.
View SolutionTwo seconds after projection, a projectile is travelling in a direction inclined at 30∘ to the horizontal. After one more second, it is travelling horizontally. Find the magnitude and direction of its velocity.
View SolutionAssertion: A body slides down an inclined plane if the angle of friction is more than the angle of the inclined plane with the horizontal.
Reason : When the angle of inclination is equal to the angle of friction, the component of weight parallel to the plane is just sufficient to overcome the frictional force.
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is
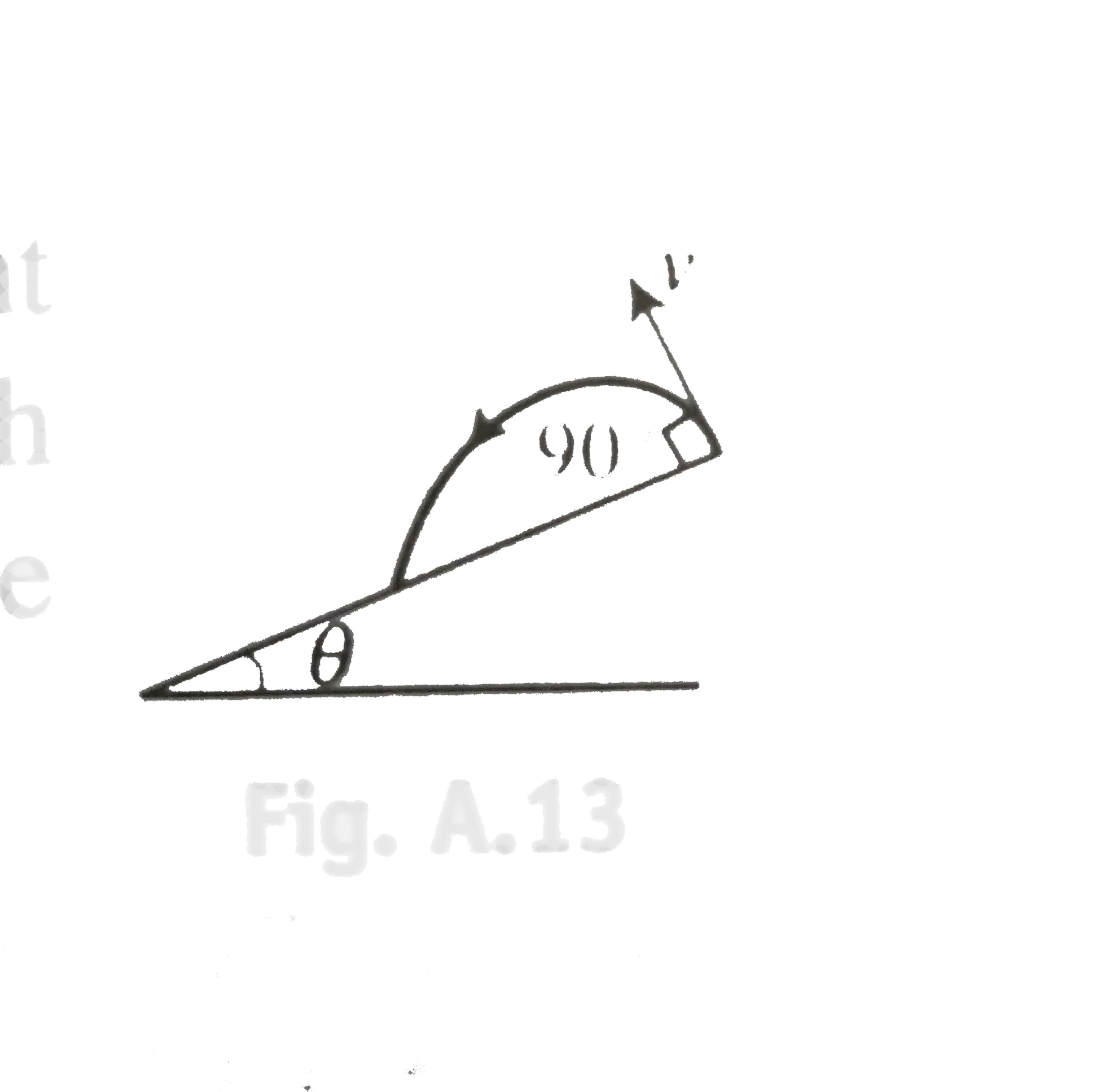
View Solution
