A vector →B which has a magnitude 8.0 is added to a vector →A which lies along the x-axis. The sum of these two vector is a third vector which lies along the y-axis and has a magnitude that is twice the magnitude of →A. Find the magnitude of →A
6√5
12√5
16√5
8√5
The correct Answer is:D
To solve the problem, we need to find the magnitude of vector →A given the conditions about vectors →A, →B, and their resultant vector →R.
1. Define the Vectors:
- Let the magnitude of vector →A be A.
- The magnitude of vector →B is given as B=8.0.
- The resultant vector →R lies along the y-axis and has a magnitude that is twice the magnitude of →A, so R=2A.
2. Use the Pythagorean Theorem:
- Since →A lies along the x-axis and →B is added to it, the resultant vector →R can be found using the Pythagorean theorem:
R2=A2+B2
- Substituting R=2A and B=8:
(2A)2=A2+82
3. Expand the Equation:
- Expanding the left side:
4A2=A2+64
4. Rearranging the Equation:
- Move A2 to the left side:
4A2−A2=64
- This simplifies to:
3A2=64
5. Solve for A2:
- Divide both sides by 3:
A2=643
6. Find A:
- Taking the square root of both sides:
A=√643=8√3≈4.62
Final Answer:
The magnitude of vector →A is 8√3 or approximately 4.62.
- Let the magnitude of vector →A be A.
- The magnitude of vector →B is given as B=8.0.
- The resultant vector →R lies along the y-axis and has a magnitude that is twice the magnitude of →A, so R=2A.
- Since →A lies along the x-axis and →B is added to it, the resultant vector →R can be found using the Pythagorean theorem:
R2=A2+B2
- Substituting R=2A and B=8:
(2A)2=A2+82
- Expanding the left side:
4A2=A2+64
- Move A2 to the left side:
4A2−A2=64
- This simplifies to:
3A2=64
- Divide both sides by 3:
A2=643
- Taking the square root of both sides:
A=√643=8√3≈4.62
The magnitude of vector →A is 8√3 or approximately 4.62.
Topper's Solved these Questions
Similar Questions
A vector ¯¯¯Qwhich has a magnitude of 8 is added to the vector ¯¯¯P which lies along the X-axis. The resultant of these two vectors is a third vector ¯¯¯R which lies along the Y-axis and has a magnitude twice that of ¯¯¯P. The magnitude of ¯¯¯P is
View SolutionA vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
View Solution
Knowledge Check
- Question 1 - Select One
The magnitude of the x-component of vector →A is 3 and the magnitude of vector →A is 5. What is the magnitude of the y-component of vector →A ?
A3B4C5D8
The sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
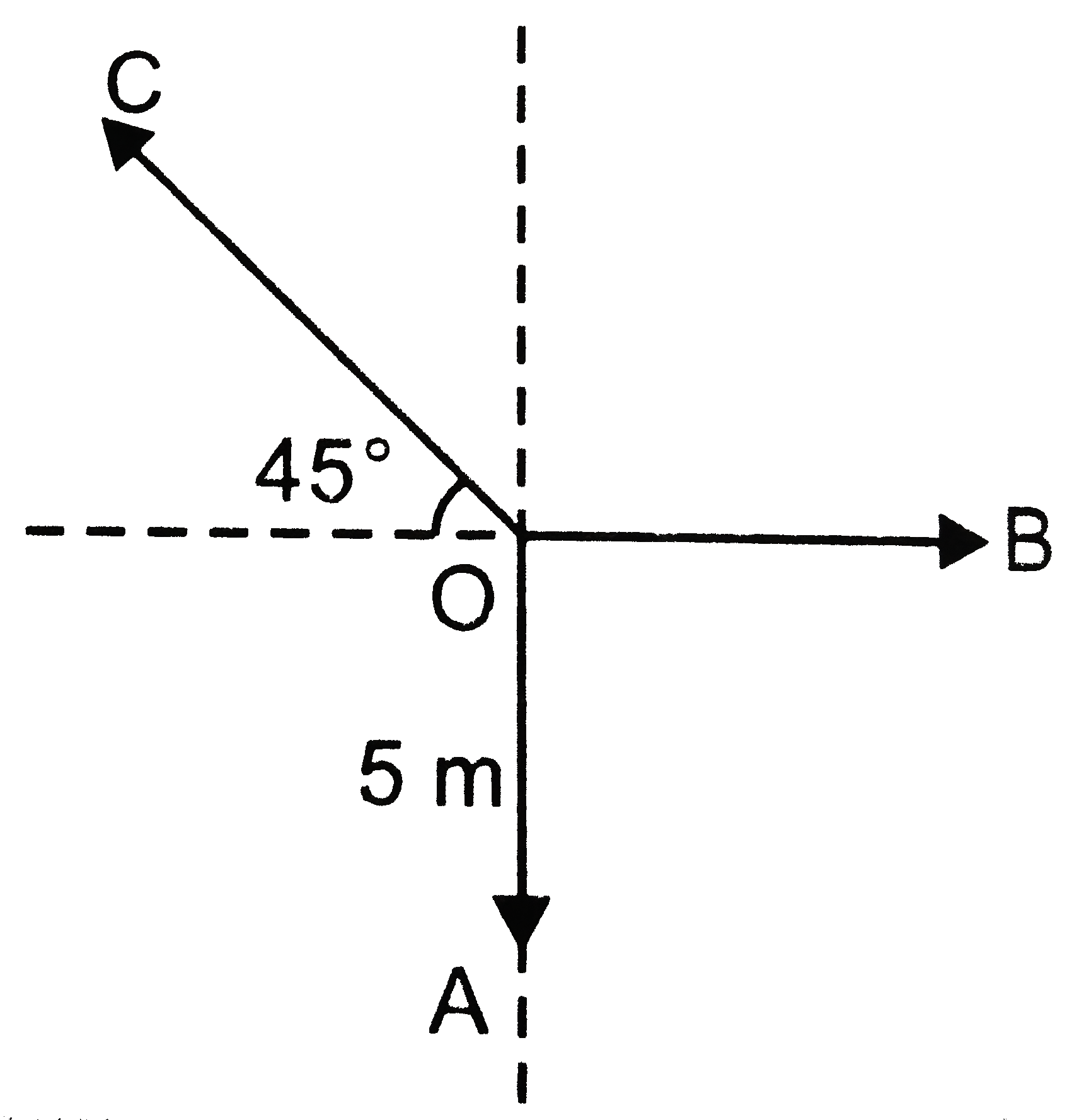 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
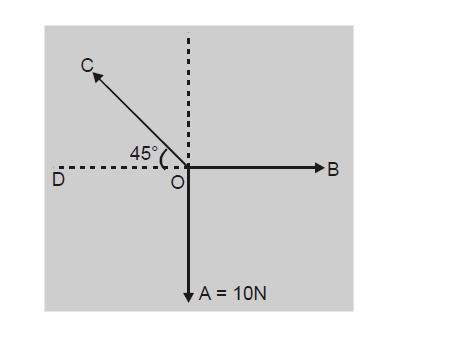
(ii) What is the magnitude of vector −−→OC ?View SolutionFind the magnitude of the sum of →Aand→B and its direction with respect to the X - axis .
View SolutionFind a Vector in the direction of →a=ˆi−2ˆj that has magnitude 7 units.
View Solution→A is a vector with magnitude A, then the unit vector ˆA in the direction →A is
View SolutionVector →A makes equal angles with x-,y-,and z-axis. Find the value of its components (in terms of magnitude of →A)
View SolutionA vector has component along the X-axis equal to 25 unit and along the Y-axis equl to 60 unit. Find the magnitude and direction of the vector.
View Solution

