What is the angle between 3a and -5a? What is the ratio of magnitude of two vectors?
The correct Answer is:A
To solve the problem, we need to find the angle between the vectors 3a and −5a, as well as the ratio of their magnitudes.
1. Identify the Vectors:
- We have two vectors: A=3a and B=−5a.
2. Determine the Direction:
- The vector 3a points in the direction of a.
- The vector −5a points in the opposite direction to a.
3. Visualize the Vectors:
- When we visualize these vectors, 3a points to the right (for example), and −5a points to the left.
4. Calculate the Angle:
- The angle between two vectors that point in opposite directions is 180∘.
- Therefore, the angle between 3a and −5a is 180∘.
5. Calculate the Magnitudes:
- The magnitude of 3a is 3.
- The magnitude of −5a is 5 (the negative sign does not affect the magnitude).
6. Find the Ratio of Magnitudes:
- The ratio of the magnitudes of the two vectors is given by:
Ratio=Magnitude of 3aMagnitude of −5a=35
Final Answers:
- The angle between 3a and −5a is 180∘.
- The ratio of the magnitudes of the two vectors is 35.
- We have two vectors: A=3a and B=−5a.
- The vector 3a points in the direction of a.
- The vector −5a points in the opposite direction to a.
- When we visualize these vectors, 3a points to the right (for example), and −5a points to the left.
- The angle between two vectors that point in opposite directions is 180∘.
- Therefore, the angle between 3a and −5a is 180∘.
- The magnitude of 3a is 3.
- The magnitude of −5a is 5 (the negative sign does not affect the magnitude).
- The ratio of the magnitudes of the two vectors is given by:
Ratio=Magnitude of 3aMagnitude of −5a=35
- The angle between 3a and −5a is 180∘.
- The ratio of the magnitudes of the two vectors is 35.
Topper's Solved these Questions
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 5.2
4 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Exercise 5.3
4 Videos
- VECTORSBOOK - DC PANDEY ENGLISHCHAPTER - VECTORSEXERCISE - Medical enrances gallery
9 Videos
- UNITS, DIMENSIONS & ERROR ANALYSIS BOOK - DC PANDEY ENGLISHCHAPTER - UNITS, DIMENSIONS & ERROR ANALYSIS EXERCISE - Medical entrances gallery
32 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
Similar Questions
The sum of three vectors shown in Fig. 2 ( c) . 77. is zero .
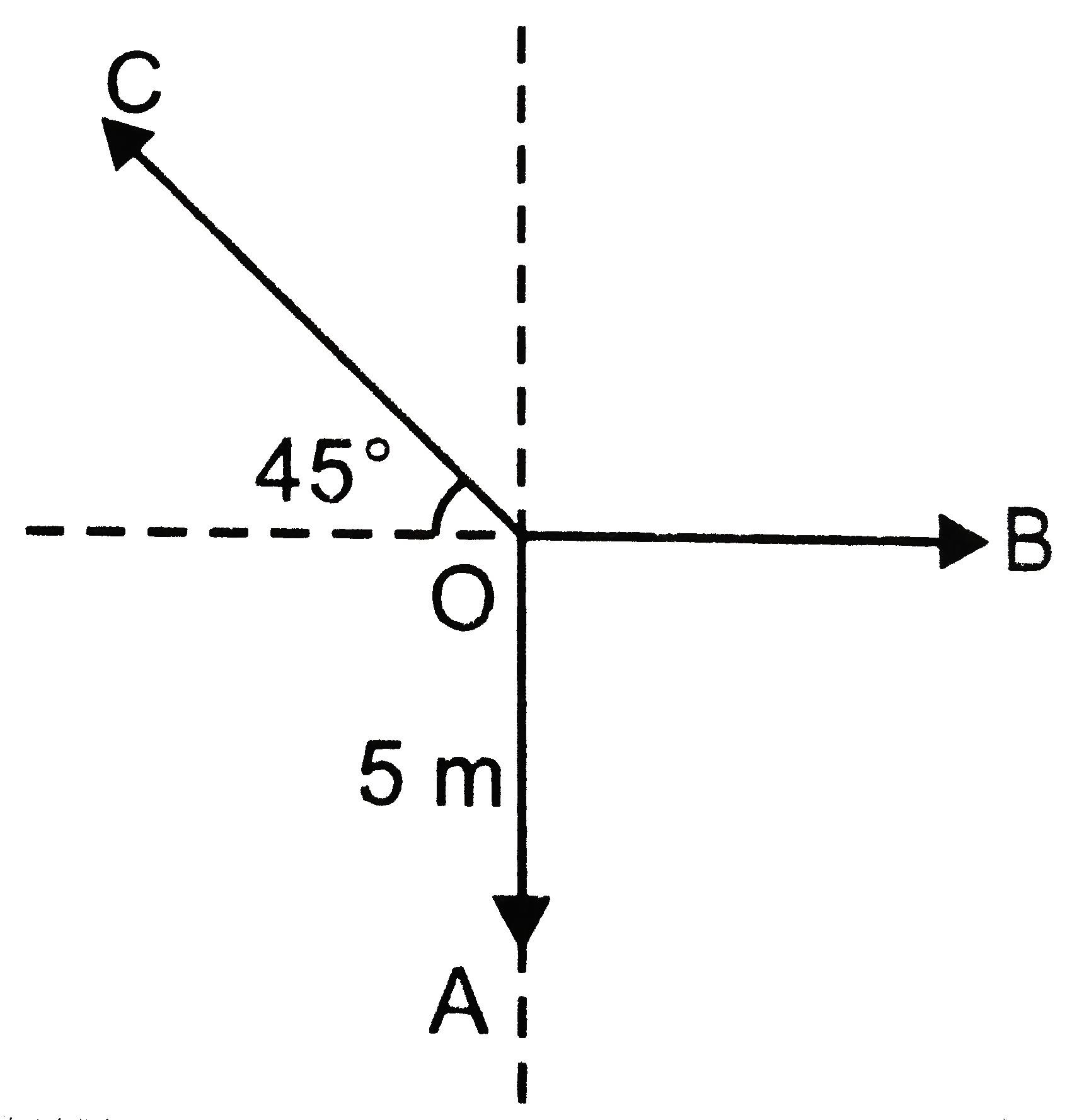 .
.
(a) What is the magnitude of the vector −−→OB?
(b) What is the magnitude of the vector −−→OC ?
View SolutionThe sum of three vectors shown in figure, is zero.
(i) What is the magnitude of vector −−→OB ?
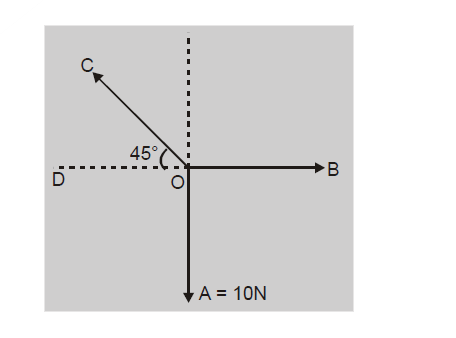
(ii) What is the magnitude of vector −−→OC ?
View SolutionWhat is the angle between vectors →a and →b with magnitudes 2 and 3 respectively ? Given →a.→b=√3 .
View SolutionWhat is the angle between two vector forces of equal magnitude such that their resultant is one-third of either of the original forces?
View SolutionIf the angle between two vectors of equal magnitude P is θ the magnitude of the difference of the vectors is
View SolutionTwo vectors have magnitudes 3 unit and 4 unit respectively. What should be the angel between them if the magnitude of the resultant ils a. 1 unit, b. 5 unit and c. 7 unit.
View SolutionTwo vectors have magnitudes 3 unit and 4 unit respectively. What should be the angel between them if the magnitude of the resultant is (a). 1 unit (b). 5 unit and (c). 7 unit.
View SolutionWhat is the angle between the vector →A and →B as shown in figure ?
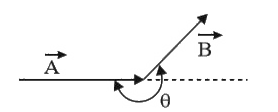
View SolutionThe resultant of two vectors at right angles is 5 N. If the angle between them is 120∘ and the resultant is √13 then the magnitude of vectors are
View SolutionTwo vectors of equal magnitude of 5 unit have an angle 600 between them. Find the magnitude of (a) the sum of the vectors and (b) the difference of the vectors.
 .
.  .
.
View Solution
