Two vectors have magnitudes 3 unit and 4 unit respectively. What should be the angel between them if the magnitude of the resultant ils a. 1 unit, b. 5 unit and c. 7 unit.
The correct Answer is:A, B, C
To solve the problem, we will use the formula for the magnitude of the resultant vector when two vectors are involved. The formula is:
R=√A2+B2+2ABcosθ
where:
- R is the magnitude of the resultant vector,
- A and B are the magnitudes of the two vectors,
- θ is the angle between the two vectors.
Given:
- A=3 units,
- B=4 units.
We will find the angle θ for three cases of the resultant vector R: 1 unit, 5 units, and 7 units.
Part (a): Resultant R=1 unit
1. Substitute the values into the formula:
1=√32+42+2⋅3⋅4cosθ
This simplifies to:
1=√9+16+24cosθ
1=√25+24cosθ
2. Square both sides:
12=25+24cosθ
1=25+24cosθ
3. Rearranging gives:
24cosθ=1−25
24cosθ=−24
4. Divide by 24:
cosθ=−1
5. Find θ:
θ=cos−1(−1)=180∘
Part (b): Resultant R=5 units
1. Substitute the values into the formula:
5=√32+42+2⋅3⋅4cosθ
This simplifies to:
5=√25+24cosθ
2. Square both sides:
52=25+24cosθ
25=25+24cosθ
3. Rearranging gives:
24cosθ=25−25
24cosθ=0
4. Divide by 24:
cosθ=0
5. Find θ:
θ=cos−1(0)=90∘
Part (c): Resultant R=7 units
1. Substitute the values into the formula:
7=√32+42+2⋅3⋅4cosθ
This simplifies to:
7=√25+24cosθ
2. Square both sides:
72=25+24cosθ
49=25+24cosθ
3. Rearranging gives:
24cosθ=49−25
24cosθ=24
4. Divide by 24:
cosθ=1
5. Find θ:
θ=cos−1(1)=0∘
Summary of Results:
- For R=1 unit, θ=180∘
- For R=5 units, θ=90∘
- For R=7 units, θ=0∘
- R is the magnitude of the resultant vector,
- A and B are the magnitudes of the two vectors,
- θ is the angle between the two vectors.
- A=3 units,
- B=4 units.
1=√32+42+2⋅3⋅4cosθ
This simplifies to:
1=√9+16+24cosθ
1=√25+24cosθ
12=25+24cosθ
1=25+24cosθ
24cosθ=1−25
24cosθ=−24
cosθ=−1
θ=cos−1(−1)=180∘
5=√32+42+2⋅3⋅4cosθ
This simplifies to:
5=√25+24cosθ
52=25+24cosθ
25=25+24cosθ
24cosθ=25−25
24cosθ=0
cosθ=0
θ=cos−1(0)=90∘
7=√32+42+2⋅3⋅4cosθ
This simplifies to:
7=√25+24cosθ
72=25+24cosθ
49=25+24cosθ
24cosθ=49−25
24cosθ=24
cosθ=1
θ=cos−1(1)=0∘
- For R=1 unit, θ=180∘
- For R=5 units, θ=90∘
- For R=7 units, θ=0∘
Topper's Solved these Questions
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Question for short Answer
14 Videos
- PHYSICS AND MATHEMATICSBOOK - HC VERMA ENGLISHCHAPTER - PHYSICS AND MATHEMATICSEXERCISE - Objective 2
5 Videos
- NEWTON'S LAWS OF MOTIONBOOK - HC VERMA ENGLISHCHAPTER - NEWTON'S LAWS OF MOTIONEXERCISE - Questions for short Answer
17 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
Similar Questions
Two vectors have magnitudes 3 unit and 4 unit respectively. What should be the angel between them if the magnitude of the resultant is (a). 1 unit (b). 5 unit and (c). 7 unit.
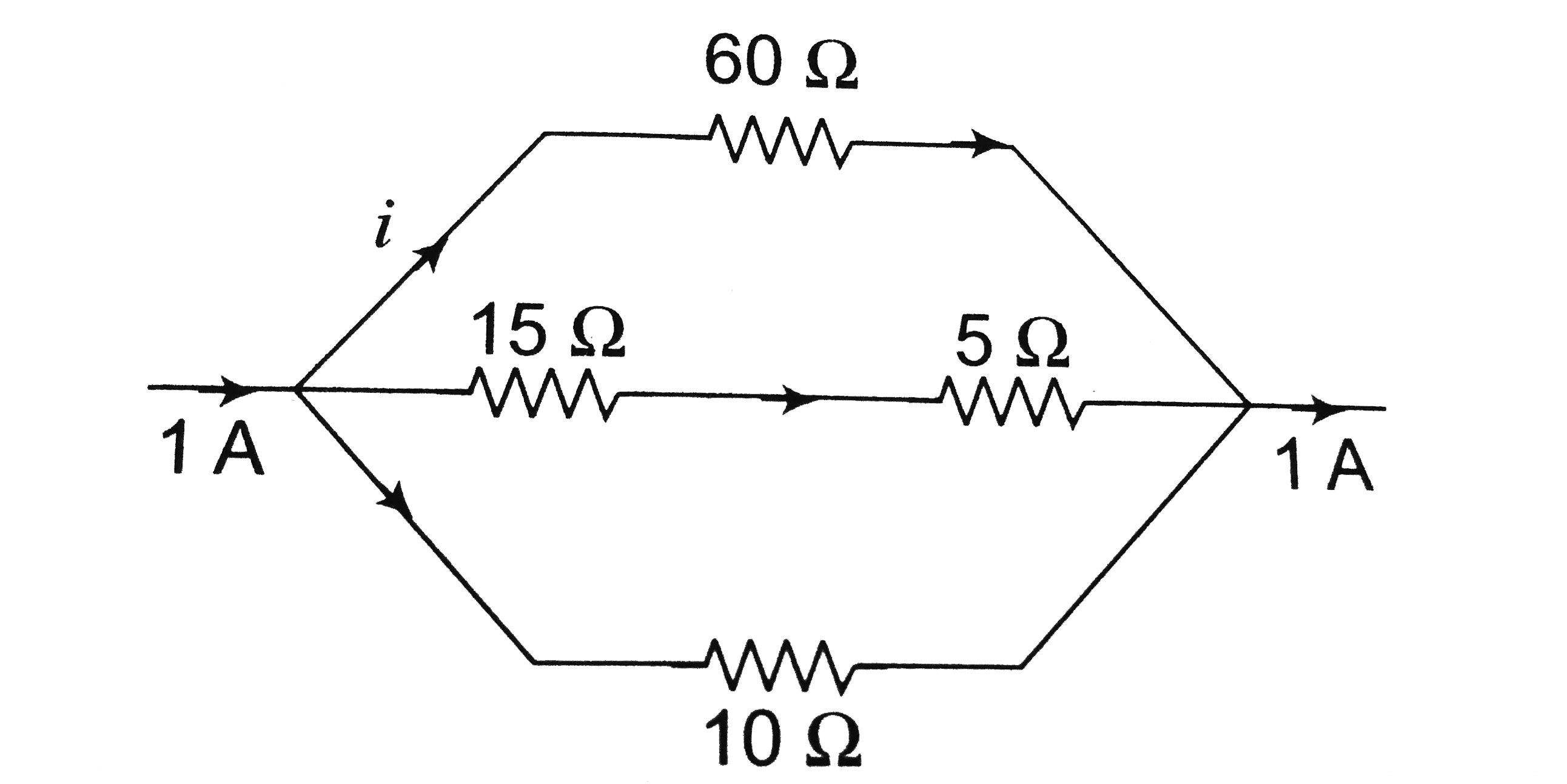
View SolutionThe magnitude in i in ampere unit is
View SolutionThe maximum and minimum magnitudes of the resultant of two vectors are 23 units and 7 units respectively. If these two vectors are acting at right angles to each other, the magnitude of their resultant will be
View SolutionThe maximum and minimum magnitudes of the resultant of two vectors are 23 units and 7 units respectively. If these two vectors are acting at right angles to each other, the magnitude of their resultant will be
View SolutionIf A=B+C have scalar magnitudes of 5,4,3 units respectively , then find the angle between A and C.
View SolutionThe maximum and minimum magnitude of the resultant of two given vectors are 17 units and 7 unit respectively. If these two vectors are at right angles to each other, the magnitude of their resultant is
View SolutionTwo vectors A and B have magnitudes 2 units and 4 units respectively. Find A. B is angle between these two vectors is (a) 0∘ (b) 60∘ (c) 90∘ (d) 120∘ .
View SolutionTwo vectors having equal magnitude of 5 units, have an angle of 60∘ between them. Find the magnitude of their resultant vector and its angle from one of the vectors.

View SolutionTwo vectors of equal magnitudes have a resultant equle to either of them, than the angel between them will be
View SolutionTwo vectors have magnitudes 6 and 8 units, respectively. Find the magnitude of the resultant vector if the angle between vectors is (a) 60∘ (b) 90∘ and ( c ) 120∘.
View Solution
