Displacement-time equation of a particle moving along x-axis is x=20+t3−12t (SI units)
(a) Find, position and velocity of particle at time t=0.
(b) State whether the motion is uniformly accelerated or not.
(c) Find position of particle when velocity of particle is zero.
The correct Answer is:A
Let's solve the problem step by step.
Given:
The displacement-time equation of a particle moving along the x-axis is:
x=20+t3−12t
(a) Find the position and velocity of the particle at time t=0.
Step 1: Find the position at t=0.
To find the position, substitute t=0 into the displacement equation:
x(0)=20+(0)3−12(0)=20+0−0=20 meters
Step 2: Find the velocity at t=0.
Velocity is the derivative of displacement with respect to time:
v=dxdt=ddt(20+t3−12t)
Differentiating:
v=0+3t2−12
Now, substitute t=0:
v(0)=3(0)2−12=0−12=−12 meters per second
(b) State whether the motion is uniformly accelerated or not.
Step 3: Find the acceleration.
Acceleration is the derivative of velocity with respect to time:
a=dvdt=ddt(3t2−12)
Differentiating:
a=6t
Since acceleration depends on time (it increases as t increases), the motion is not uniformly accelerated.
(c) Find the position of the particle when the velocity of the particle is zero.
Step 4: Set the velocity equation to zero and solve for t.
From the velocity equation:
v=3t2−12=0
Solving for t:
3t2=12⟹t2=4⟹t=±2
Since time cannot be negative, we take t=2 seconds.
Step 5: Find the position at t=2 seconds.
Substituting t=2 into the displacement equation:
x(2)=20+(2)3−12(2)=20+8−24=20−16=4 meters
Summary of Answers:
(a) Position at t=0 is 20 meters, velocity at t=0 is −12 m/s.
(b) The motion is not uniformly accelerated.
(c) The position when the velocity is zero is 4 meters.
The displacement-time equation of a particle moving along the x-axis is:
x=20+t3−12t
To find the position, substitute t=0 into the displacement equation:
x(0)=20+(0)3−12(0)=20+0−0=20 meters
Velocity is the derivative of displacement with respect to time:
v=dxdt=ddt(20+t3−12t)
Differentiating:
v=0+3t2−12
Now, substitute t=0:
v(0)=3(0)2−12=0−12=−12 meters per second
Acceleration is the derivative of velocity with respect to time:
a=dvdt=ddt(3t2−12)
Differentiating:
a=6t
Since acceleration depends on time (it increases as t increases), the motion is not uniformly accelerated.
From the velocity equation:
v=3t2−12=0
Solving for t:
3t2=12⟹t2=4⟹t=±2
Since time cannot be negative, we take t=2 seconds.
Substituting t=2 into the displacement equation:
x(2)=20+(2)3−12(2)=20+8−24=20−16=4 meters
(a) Position at t=0 is 20 meters, velocity at t=0 is −12 m/s.
(b) The motion is not uniformly accelerated.
(c) The position when the velocity is zero is 4 meters.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 11videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 21videos
KINEMATICS
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises45videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE15videos
KINEMATICS 1
Similar Questions
Find the time t0 when x-coordinate of the particle is zero.
View SolutionIf the velocity of a particle moving along x-axis is given as v=(3t2−2t) and t=0, x=0 then calculate position of the particle at t=2sec.
View SolutionThe position of a particle moving along x-axis given by x=(−2t3−3t2+5)m. The acceleration of particle at the instant its velocity becomes zero is
View SolutionThe displacement x of a particle moving along x-axis at time t is given by x2=2t2+6t. The velocity at any time t is
View SolutionThe acceleration - time graph for a particle moving along x - axis is shown in figure, If the initial velocity of particle is −5m/s, the velocity at t = 8 s is
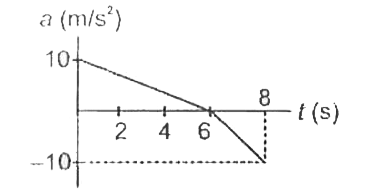 View Solution
View SolutionFigure shows the displacement-time graph of a particle moving in a straight line. Find the signs of velocity and acceleration of particle at time t=t1andt=t2.
 View Solution
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
 View Solution
View SolutionThe acceleration-time graph of a particle moving along x-axis is shown in the figure. If the particle starts with velocity 3 m/s at t = 0, find the velocity of particle at t = 4 s.
 View Solution
View Solutionx-coordinate of a particle moving along this axis is x=(2+t2+2t3). Here, x is in meres and t in seconds. Find (a) position of particle from where it started its journey, (b) initial velocity of particle and (c) acceleration of particle at t=2s.
View SolutionThe position (x) of a particle moving along x - axis veries with time (t) as shown in figure. The average acceleration of particle in time interval t = 0 to t = 8 s is
 View Solution
View Solution

