Velocity of a particle in x-y plane at any time t is v=(2tˆi+3t2ˆj)m/s At t=0, particle starts from the co-ordinates (2m,4m). Find
(a) acceleration of the particle at t=1s.
(b) position vector and co-ordinates of the particle at t=2s.
The correct Answer is:A, B, C, D
(a) a=dvdt=ddt(2tˆi+3t2ˆj)
=(2ˆi++6tˆj)m/s2
At t=1s,
a=(2ˆi+6ˆj)m/s2
(b) intds=intv dt
or s=∫vdt=∫(2tˆi+3t2ˆj)dt
∴rf−ri=∫finalintitial(2tˆi+3t2ˆj)dt
orr2sec−r0sec=∫20(2tˆi+3t2ˆj)dt
∴r2sec=r0sec+[t2ˆi+t3ˆj]20
=(2ˆi+4ˆj)+(4ˆi+8ˆj)
=(6ˆi+12ˆj)m
Therefore, coordinates of the particle at t=2s are (6m,12m)
Topper's Solved these Questions
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 1
1 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - Example Type 2
1 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
Similar Questions
Acceleration of a particle in x-y plane varies with time as a=(2tˆi+3t2ˆj)m/s2 At time t=0, velocity of particle is 2m/s along positive x direction and particle starts from origin. Find velocity and coordinates of particle at t=1s.
View SolutionAcceleration of a particle at any time t is →a=(2tˆi+3t2ˆj)m/s2.If initially particle is at rest, find the velocity of the particle at time t=2s
View SolutionThe coordinates of a particle moving in x-y plane at any time t are (2t,t2). Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
View SolutionA particle is moving with a velocity of v=(3+6t+9t2)ms. Find out
(a) the acceleration of the particle at t=3s.
(b) the displacement of the particle in the interval t=5s to t=8s.
View SolutionVelocity of a particle at any time t is v=(2ˆi+2tˆj)m/s. Find acceleration and displacement of particle at t=1s. Can we apply v=u+at or not?
View SolutionVelocity (in m/s) of a particle moving along x-axis varies with time as, v=(10+5t−t2) At time t=0,x=0. Find
(a) acceleration of particle at t=2s and
(b) x-coordinate of particle at t=3s
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionVelocity-time graph of a particle moving in a straight line is shown in figure. At time t=0, displacement of the particle from mean position is 10 m. Find
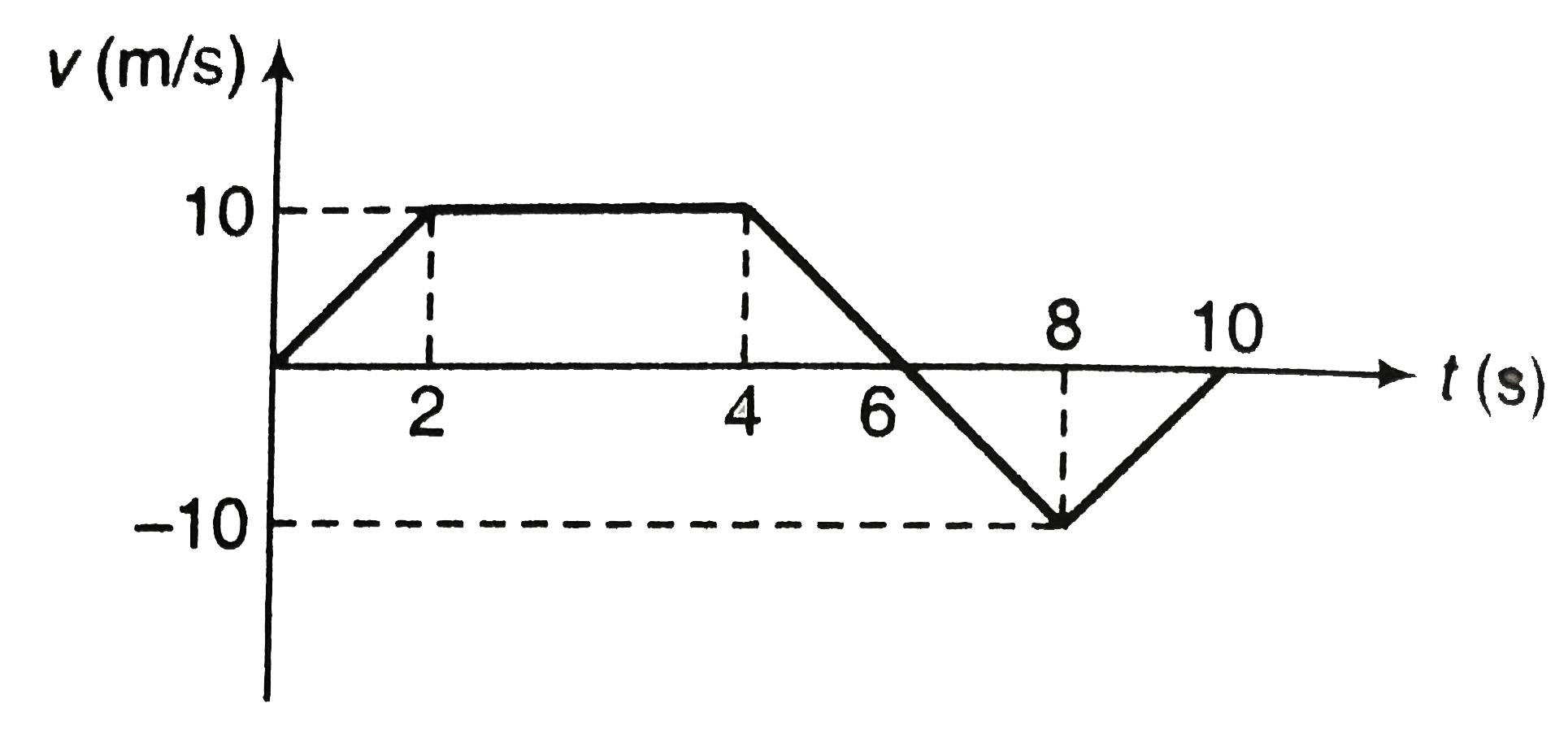
(a) acceleration of particle at t=1s,3sand9s.
(b) position of particle from mean position at t=10s.
(c) write down s-t equation for time interval (i)0≤t≤2s, (ii) 4s≤t≤8s
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View SolutionA particle starts from rest and moves with an acceleration of a={2+|t−2|}m/s2 The velocity of the particle at t=4 sec is
View Solution
