Question

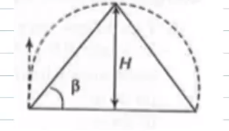
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If ${\displaystyle \alpha \text{and}\beta }$ be the base angles and ${\displaystyle \theta }$ the angle of projection, prove that ${\displaystyle \tan \theta =\tan \alpha +\tan \beta }$ .

Answer

A

Explanation

The situation is shown in figure.

From figure, we have
`tan alpha + tan beta = y/x + y/(R-x)`
`tan alpha + tan beta = (yR)/(x(R-x))`……….(i)
Equation of trajectory is
`y = x tan theta [1-x/R]`
or, ` tan theta = (yR)/(x(R-x))` ........(ii)
From Eqs. (i) and (ii), we have
`tan theta = tan alpha + tan beta`