A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If 30∘and60∘ be the base angles and θ the angle of projection then tanθ is
2√3
4√3
13
3
The correct Answer is:B
To solve the problem step by step, we will analyze the situation involving the triangle and the projectile motion of the particle.
Step 1: Understand the Geometry of the Triangle
We have a triangle with base angles of 30∘ and 60∘. Let's denote the vertices of the triangle as A, B, and C, where C is the vertex opposite the base AB. The height from C to the base AB will be denoted as CD.
Step 2: Draw the Perpendicular
From point C, draw a perpendicular CD to the base AB. Let D be the foot of the perpendicular. The lengths of the segments on the base can be defined as follows:
- Let AD=x
- Let DB=r−x where r is the length of the base AB
Step 3: Use Trigonometric Ratios
Using the angles of the triangle:
- For angle C (which is 90∘), we can use the tangent function for angles 30∘ and 60∘:
tan30∘=CDAD=yx
tan60∘=CDDB=yr−x
Step 4: Set Up the Equations
From the definitions above, we have:
- y=xtan30∘=x√3
- y=(r−x)tan60∘=(r−x)√3
Step 5: Equate the Two Expressions for y
Setting the two expressions for y equal to each other:
x√3=(r−x)√3
Step 6: Solve for x
Cross-multiplying gives:
x=(r−x)⋅3
x+3x=3r
4x=3r⟹x=3r4
Step 7: Substitute Back to Find y
Substituting x back into the equation for y:
y=3r4√3
Step 8: Find tanθ
Now we can find tanθ:
tanθ=yx=3r4√33r4=1√3=tan30∘
Step 9: Use the Trajectory Equation
Using the trajectory equation:
y=xtanθ(1−xr)
From this, we can derive that:
tanθ=tan30∘+tan60∘
Step 10: Calculate tanθ
Calculating the sum:
tan30∘+tan60∘=1√3+√3=1+3√3=4√3
Final Answer
Thus, the value of tanθ is:
4√3
We have a triangle with base angles of 30∘ and 60∘. Let's denote the vertices of the triangle as A, B, and C, where C is the vertex opposite the base AB. The height from C to the base AB will be denoted as CD.
From point C, draw a perpendicular CD to the base AB. Let D be the foot of the perpendicular. The lengths of the segments on the base can be defined as follows:
- Let AD=x
- Let DB=r−x where r is the length of the base AB
Using the angles of the triangle:
- For angle C (which is 90∘), we can use the tangent function for angles 30∘ and 60∘:
tan30∘=CDAD=yx
tan60∘=CDDB=yr−x
From the definitions above, we have:
- y=xtan30∘=x√3
- y=(r−x)tan60∘=(r−x)√3
Setting the two expressions for y equal to each other:
x√3=(r−x)√3
Cross-multiplying gives:
x=(r−x)⋅3
x+3x=3r
4x=3r⟹x=3r4
Substituting x back into the equation for y:
y=3r4√3
Now we can find tanθ:
tanθ=yx=3r4√33r4=1√3=tan30∘
Using the trajectory equation:
y=xtanθ(1−xr)
From this, we can derive that:
tanθ=tan30∘+tan60∘
Calculating the sum:
tan30∘+tan60∘=1√3+√3=1+3√3=4√3
Thus, the value of tanθ is:
4√3
Similar Questions
A particle is thrown over a triangle from one end of a horizontal base and after grazing the vertex falls on the other end of the base. If αandβ be the base angles and θ the angle of projection, prove that tanθ=tanα+tanβ .
View SolutionIn an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
View Solution
Knowledge Check
In a certain isosceles triangle , the measure of the vertex angle is four times the measure of each of the base angles , what is the measure , in degrees, of the vertex angle ?
A30∘B45∘C60∘D120∘
Two parallel straight lines are inclined to the horizon at an angle ∝. A particle is projected from a point mid way between them so as to graze one of the lines and strikes the other at right angle. Show that if θ is the angle between the direction of projection and either of lines, then tanθ=(√2−1)cot∝.
View SolutionIf the base of a triangle and the ratio of tangent of half of base angles are given, then identify the locus of the opposite vertex.
View SolutionIf the base of a triangle and the ratio of tangent of half of base angles are given, then identify the locus of the opposite vertex.
View SolutionA particle is projected with speed u at angle θ to the horizontal. Find the radius of curvature at highest point of its trajectory
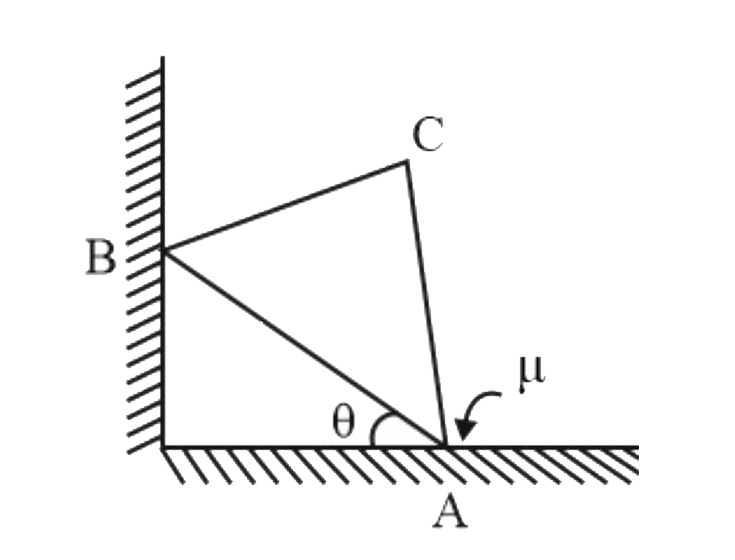
View SolutionA thin uniform equilateral plate rests in a vertical plane with one of its vertex A on a rough horizontal floor and another vertex B on a smooth vertical wall. If the coefficient of friction μ=1√3, then the least angle θ its base AB can make with the horizontal surface is
View SolutionA particle is projected at angle θ with horizontal from ground. The slop (m) of the trajectory of the particle varies with time (t) as
View SolutionA stone projected at angle θ with horizontal from the roof of a tall building falls on the ground after three seconds. Two second after the projection it was again at the level of projection. Then the height of the building
View Solution
