In the figure sown in the concept, find
(a) Equilbrium extension x∘(=AB)
(b) Maximum extension xm(=AC)
(c)Maximum speed at point B.
The correct Answer is:B
(a) At point B,
Fnet=0
⇒kx0=mg
⇒x0mgK
 .
.
From A to C (vA=vC=0)
Decreasing in gravitational potential energy = incrasing in spring energy.
∴mgxm=−12Kx2m,AC=xm
⇒xm=2mgK
(c) Form A to B
Dereasing ingravitational potential energy = increasing in (spring potential energy + kinetic energy)
⇒mgx0=12Kx20+12mv2max
Substituting the value of x0=mgK in the above eqation, we get
vmax=(√mK)g.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Miscellaneous Example
6 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Exercise 9.1
10 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Solved Examples
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
In the adjoining figure,AB=AC.Find the value of x
View SolutionA block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.
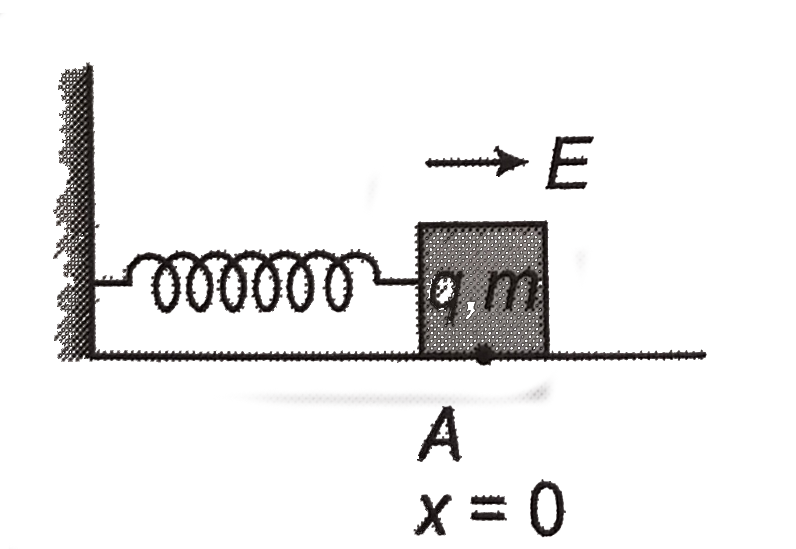
View Solution
Knowledge Check
Block A in the figure is released from the rest when the extension in the spring is x0. The maximum downward displacement of the block will be :
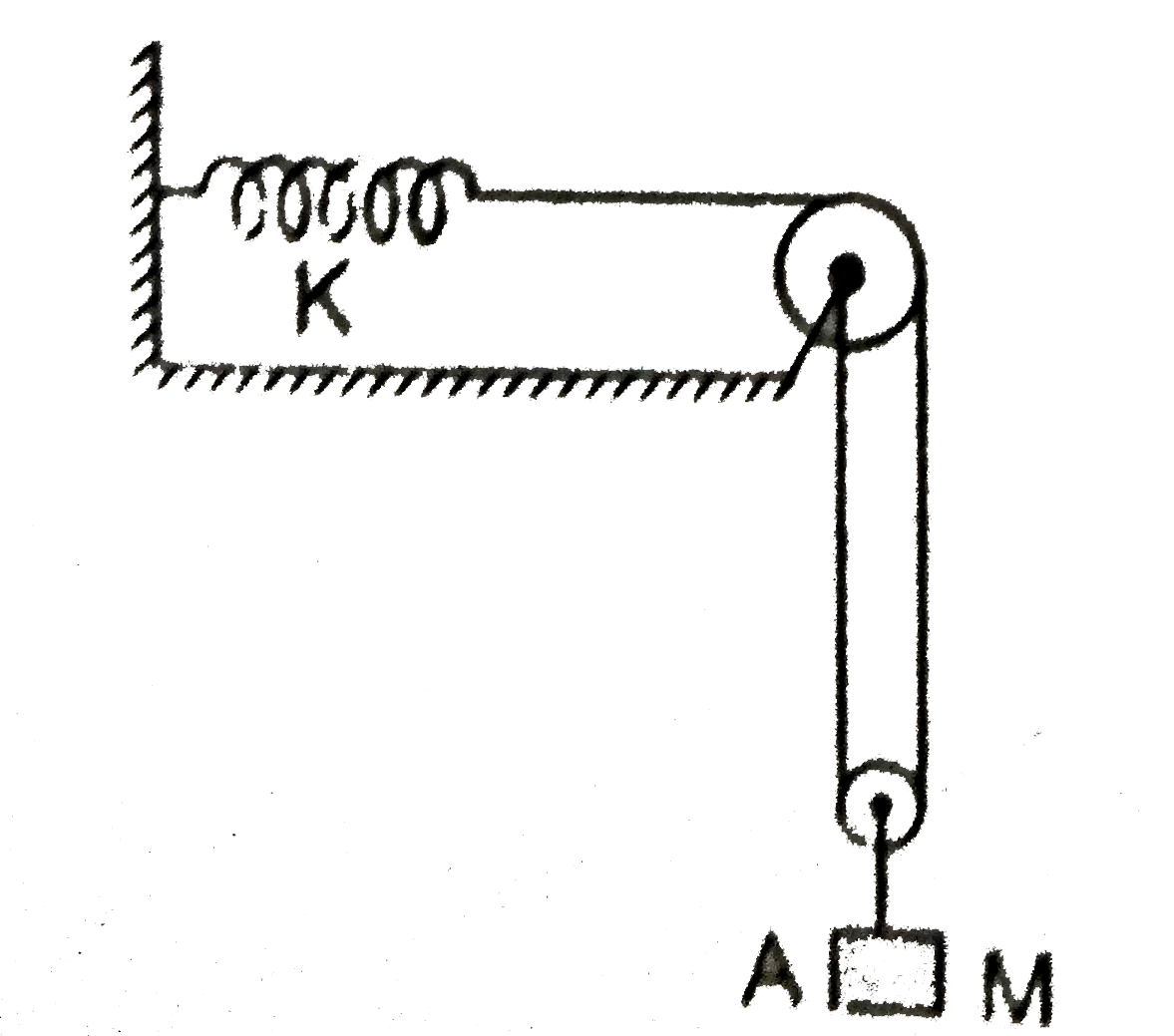 AMg/2k−x0BMg/2k+x0C2Mg/k−x0D2Mg/k+x0
AMg/2k−x0BMg/2k+x0C2Mg/k−x0D2Mg/k+x0Block A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :
 A2MgK−2x0BMg2K+x0C2MgK−x0D2MgK+x0
A2MgK−2x0BMg2K+x0C2MgK−x0D2MgK+x0
A block of mass m having charge q is attached to a spring of spring constant k. This arrangement is placed in uniform electric field E on smooth horizontal surface as shown in the figure. Initially spring in unstretched. Find the extension of spring in equilibrium position and maximum extension of spring.

View SolutionConsider the situation shown in figure.
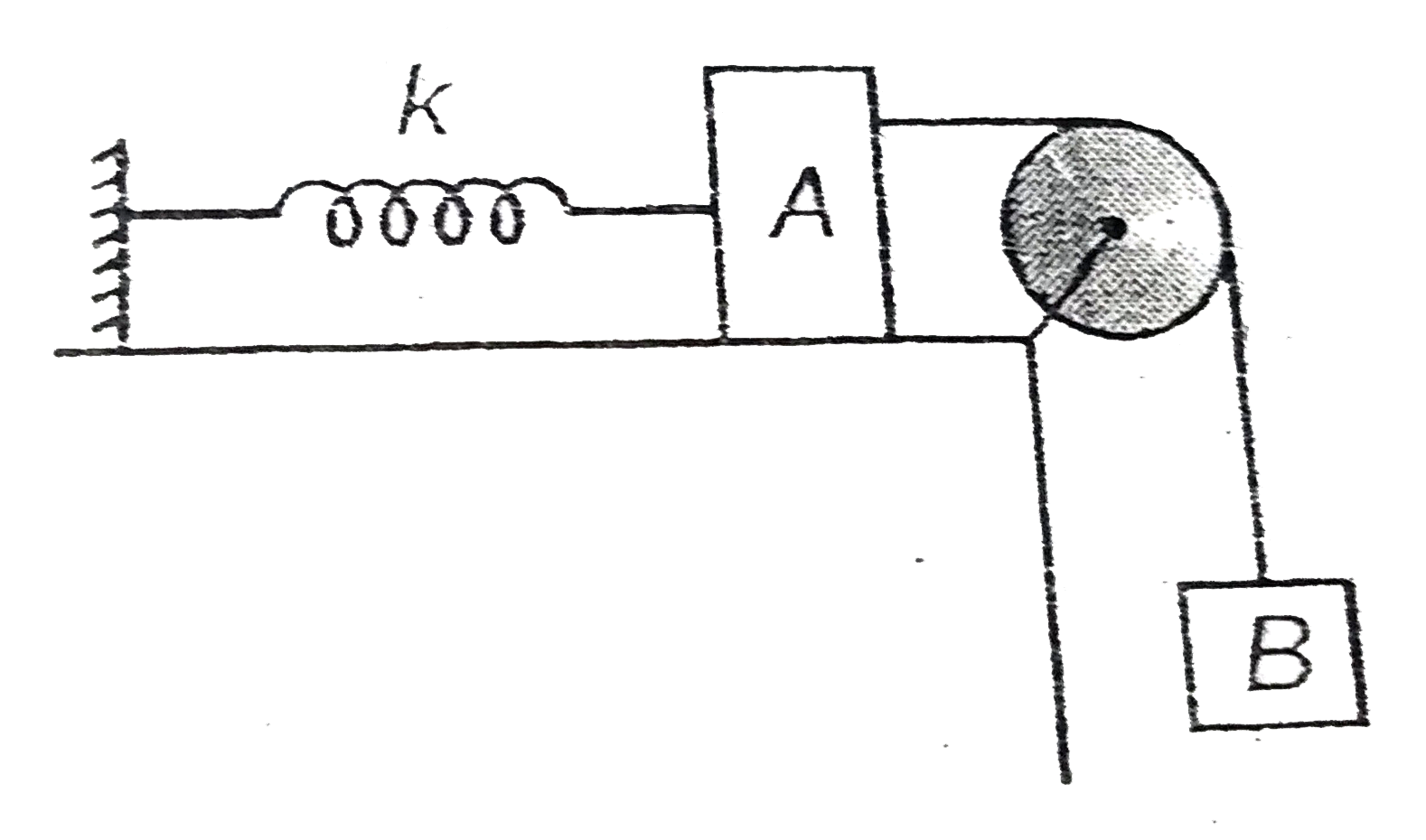
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionConsider the situation shown in figure.

Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionBlock A in the figure is released from rest when the extension in the spring is x0(x0<mg/k). The maximum downward displacement of the block is (there is no friction) :

View Solution_S01_010_Q01.png)
Hanger is mass less a ball of mass m drops a height h which sticks to hanger after striking. Neglect over turning find out the maximum extension in rod. Assuming or id massless let maximum extension be xmax.
View Solution_S01_010_Q01.png)
Hanger is mass less a ball of mass m drops a height h which sticks to hanger after striking. Neglect over turning find out the maximum extension in rod. Assuming or id massless let maximum extension be xmax.
View Solution
