The total work done on a particle is equal to the change in its kinetic energy
always
only if the forces acting on the body are conservative
only in the inertial force frame
only if no external force is acting
The correct Answer is:A
To solve the question, "The total work done on a particle is equal to the change in its kinetic energy," we can follow these steps:
Step 1: Understand the Work-Energy Theorem
The Work-Energy Theorem states that the total work done on a particle is equal to the change in its kinetic energy. Mathematically, this can be expressed as:
W=ΔKE
where W is the work done, and ΔKE is the change in kinetic energy.
Step 2: Define Kinetic Energy
Kinetic energy (KE) of a particle is given by the formula:
KE=12mv2
where m is the mass of the particle and v is its velocity.
Step 3: Analyze the Change in Kinetic Energy
The change in kinetic energy when a particle goes from an initial velocity vi to a final velocity vf can be calculated as:
ΔKE=KEf−KEi=12mv2f−12mv2i
Step 4: Apply the Work-Energy Theorem
According to the Work-Energy Theorem, the total work done on the particle (which can include both conservative and non-conservative forces) results in the change in kinetic energy:
W=ΔKE
This holds true regardless of the type of forces acting on the particle.
Step 5: Conclusion
From the analysis, we conclude that the statement "The total work done on a particle is equal to the change in its kinetic energy" is true in all scenarios, provided we consider all forces acting on the particle. Therefore, the correct answer to the question is:
Always.
The Work-Energy Theorem states that the total work done on a particle is equal to the change in its kinetic energy. Mathematically, this can be expressed as:
W=ΔKE
where W is the work done, and ΔKE is the change in kinetic energy.
Kinetic energy (KE) of a particle is given by the formula:
KE=12mv2
where m is the mass of the particle and v is its velocity.
The change in kinetic energy when a particle goes from an initial velocity vi to a final velocity vf can be calculated as:
ΔKE=KEf−KEi=12mv2f−12mv2i
According to the Work-Energy Theorem, the total work done on the particle (which can include both conservative and non-conservative forces) results in the change in kinetic energy:
W=ΔKE
This holds true regardless of the type of forces acting on the particle.
From the analysis, we conclude that the statement "The total work done on a particle is equal to the change in its kinetic energy" is true in all scenarios, provided we consider all forces acting on the particle. Therefore, the correct answer to the question is:
Always.
Topper's Solved these Questions
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 subjective
27 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 2 Objective
30 Videos
- WORK, ENERGY & POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY & POWEREXERCISE - Level 1 Assertion And Reason
12 Videos
- WAVE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - WAVE MOTIONEXERCISE - Integer Type Question
11 Videos
- WORK, ENERGY AND POWERBOOK - DC PANDEY ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - MEDICAL ENTRACES GALLERY
33 Videos
Similar Questions
The total work done on a particle is equal to the change in its mechanical energy
View SolutionSTATEMENT-1: Work done by the net force acting on a particle is equal to the change in its kinetic energy.
STATEMENT-2: Change in potential energy is always equal to the work done by external forces.
STATEMENT-3: Work energy theorem is not applicable, if the work is done by the non-conservative forces
View SolutionAssertion :− According work energy theorem net work done on a body is equal to change in its kinetic energy.
Reason :− The work energy theorem is independent of Newton's second law.
View SolutionShow that the work done to rotate a body is equal to the change in rotational kinetic energy,
View SolutionStatement−1: The work done by all forces on a system equals to the change in kinetic energy of that system . This statement is true even if nonconservative forces act on the system.
Statement −2: The total work done by internal forces may be positive.
View SolutionWork energy theorem sys work done by all the force is equal to change in kinetic energy" In the diagram, a disc of mass M and radius Ris rolling without slipping on a rough fixed inclined AB=l,V= velocity of disc at B.
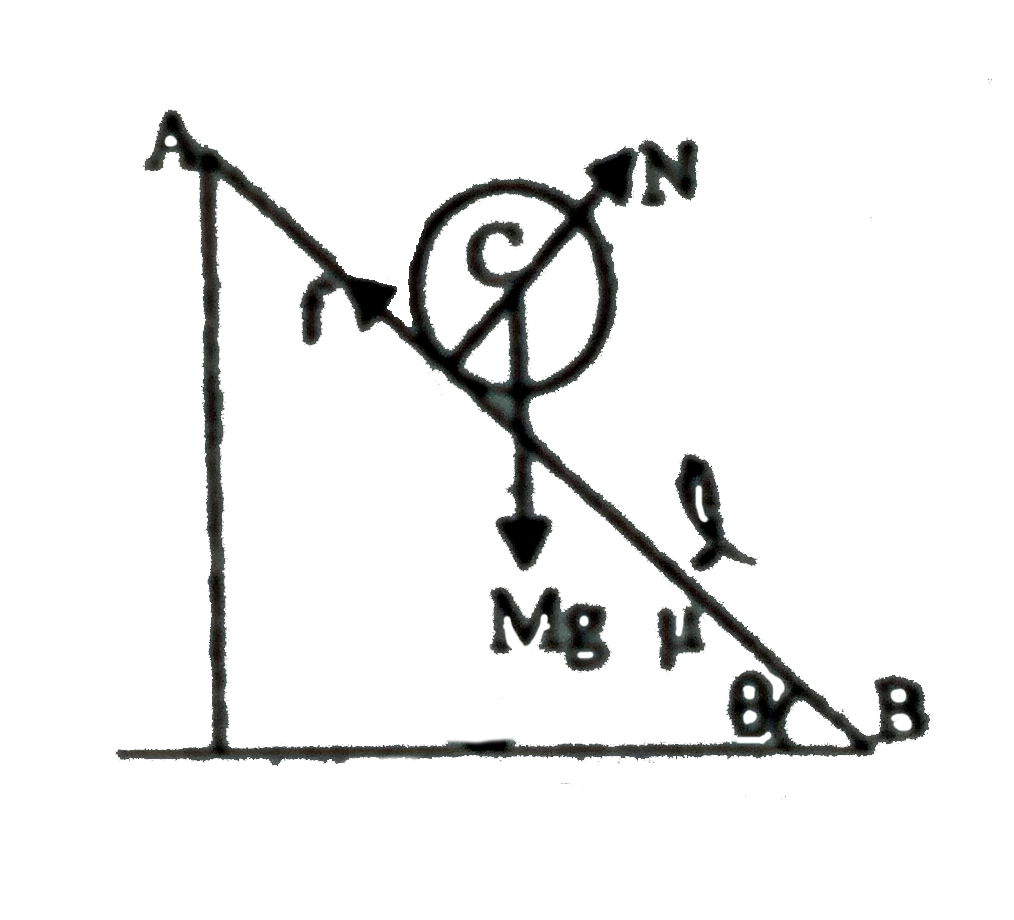
Choose the correct option(s)
View SolutionWork energy theorem sys"work done by all the force is equal to change in kinetic energy" In the diagram, a disc of mass M and radius Ris rolling without slipping on a rough fixed inclined AB=l,V= velocity of disc at B.
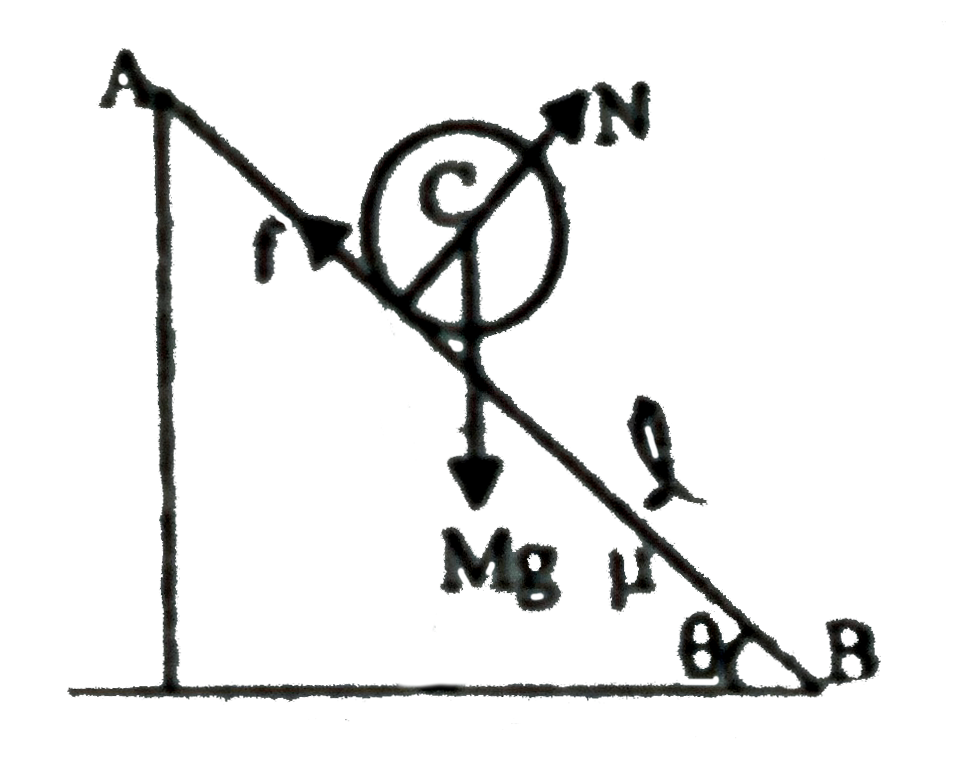
Choose the correct option(s)
View SolutionAsseration : Displacement time graph of a particle moving in a straight line is shown in figure. Work done by all the forces between time interval t1 and t2 is definitely zero.
 ,
,
Reason : Work done by all the forces is equal to change in kinetic energy.
View SolutionA particle executes linear SHM with amplitude A and mean position is x=0. Determine position of the particle where potential energy of the particle is equal to its kinetic energy.
View SolutionA body of mass 2.0 kg initially at rest is moved by a horizontal force of 0.50 N on a smooth table. Find the work done by the force in 8.0 s and show that this equals the change in the kinetic energy of the body.
View Solution
