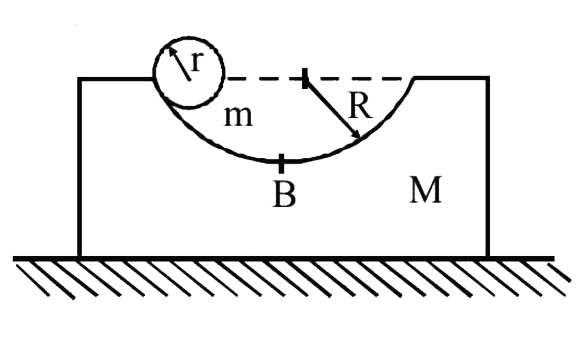
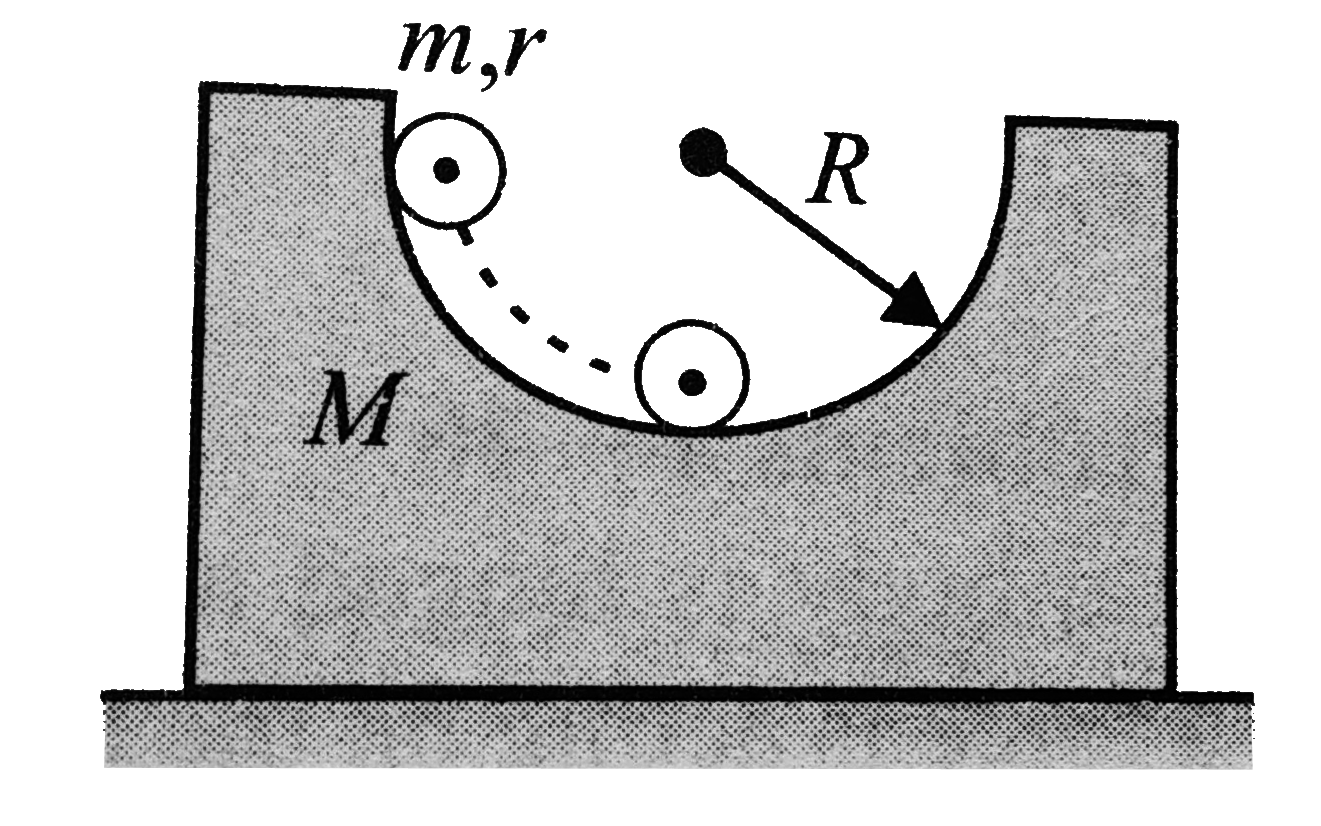
A block of mass M with a semicircualr of radius R, rests on a horizontal frictionless surface. A uniform cylinder of radius r and mass m is released from rest the top point A The cylinder slips on the semicircular frictionless track. How far has the block moved when the cylinder reaches the bottom (point B) of the track ? How fast is the block moving when the cylinder reaches the bottom of the track?
The correct Answer is:B
(i) 
Mx=m(R−r−x)
∴x=m(R−r)M+m
(ii) 
∴√2KMM=√2Kmm
∴KMKm=mM …(i)
Km+Km= decrease in potential energy of m
=mg(R−r) ...(ii)
Solving these two equations we get,
KM=(mM+m)mg(R−r)=12Mv2M
∴vM=m√2g(R−r)M(M+m)
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
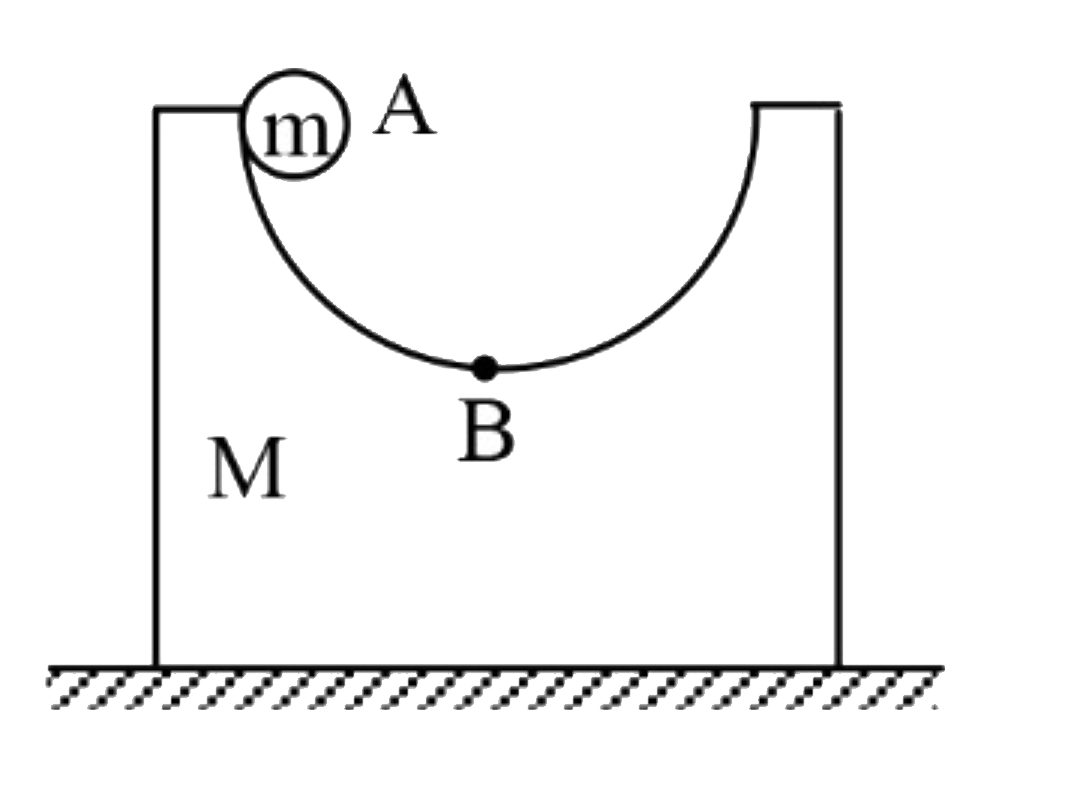
A block of mass M = 2 kg with a semicircular track of radius R = 1.1 m rests on a horizontal frictionless surface. A uniform cylinder of radius r = 10 cm and mass = 1.0 kg is released from rest from the top point A. the cylinder slips on the semicircular frictionless track. The speed of the block when the cylinder reaches the bottom of the track at B is (g=10ms−2)
View SolutionA block of mass M with a semi - circular track of radius R rests on a smooth floor. A sphere of mass m and radius r is released from rest from A. Find the velocity of sphere and track , when the sphere reaches B.

View Solution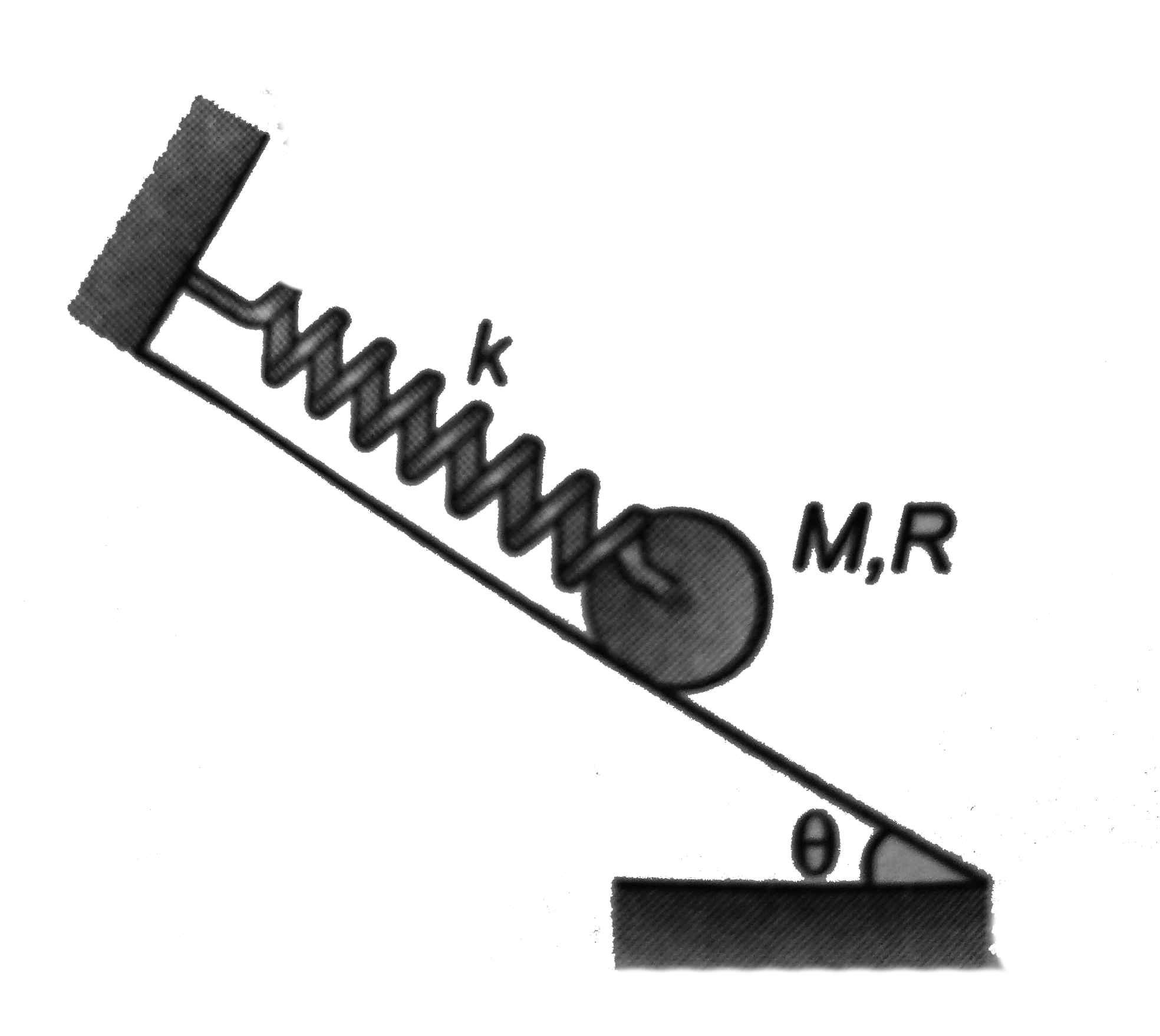
A uniform cylinder of mass M and radius R is released from rest on a rough inclined surface of inclination θ with the horizontal as shown in figure. As the cylinder rolls down the inclined surface, the maximum elongation it the spring stiffness k is
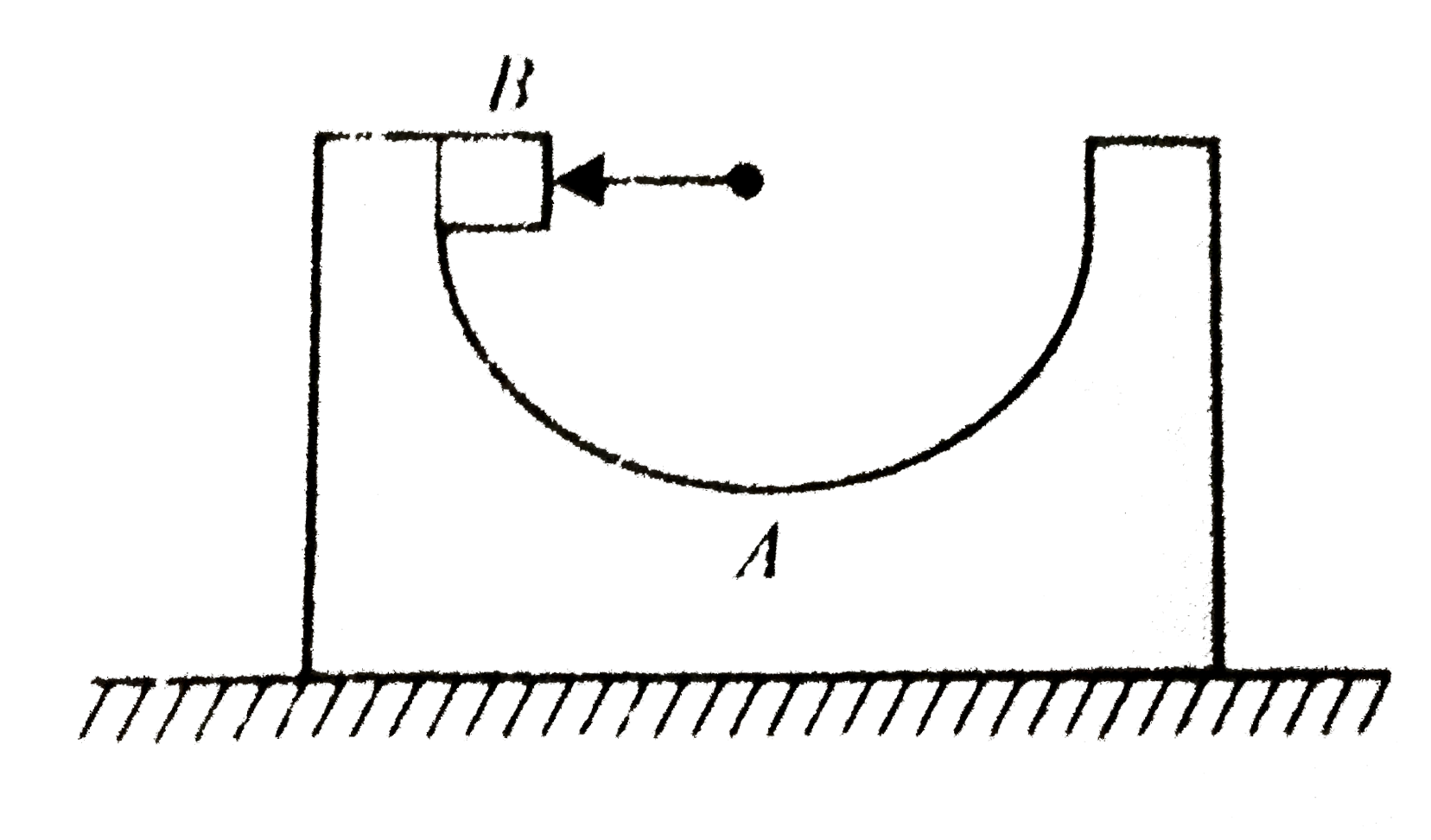
View SolutionFigure shows a block A of mass 6m having a smooth semicircular groove of radius a placed on a smooth horizontal surface. A block B of mass m is released from a position in groove where its radius is horizontal. Find the speed of the bigger block when the smaller block reaches its bottom most position.
View SolutionA block of mass m slides along a frictionless surface as shown in the figure. If it is releases from rest from A what is its speed at B?

View SolutionUniform solid cylinder of mass m and radius R is placed on a rough horizontal surface. A horizontal constant force is applied at the top point P of the cylinder so that it start pure rolling .In the above question, the frictional force on the cylinder is
View SolutionA uniform solid cylinder of mass 2kg and radius 0.2m is released from rest at the top of a semicircular track of radius 0.7m cut in a block of mass M=3kg as shown in Fig. The block is resting on a smooth horizontal surface and the cylinder rolls down without slipping. Based on the above information, answer the following questions:
The speed of the point of contact of the cylinder with the block w.r.t. ground, when the cylinder reaches the bottom of the track is
View SolutionA mass M is supported by a massless string wound round a uniform cylinder ofmass M and radius R. On releasing the mass from rest, it will fall with acceleration?

View SolutionA cylinder is released from rest from the top of an incline of inclination θ and length 'L'. If the cylinder rolls without slipping. What will be its speed when it reaches the bottom?
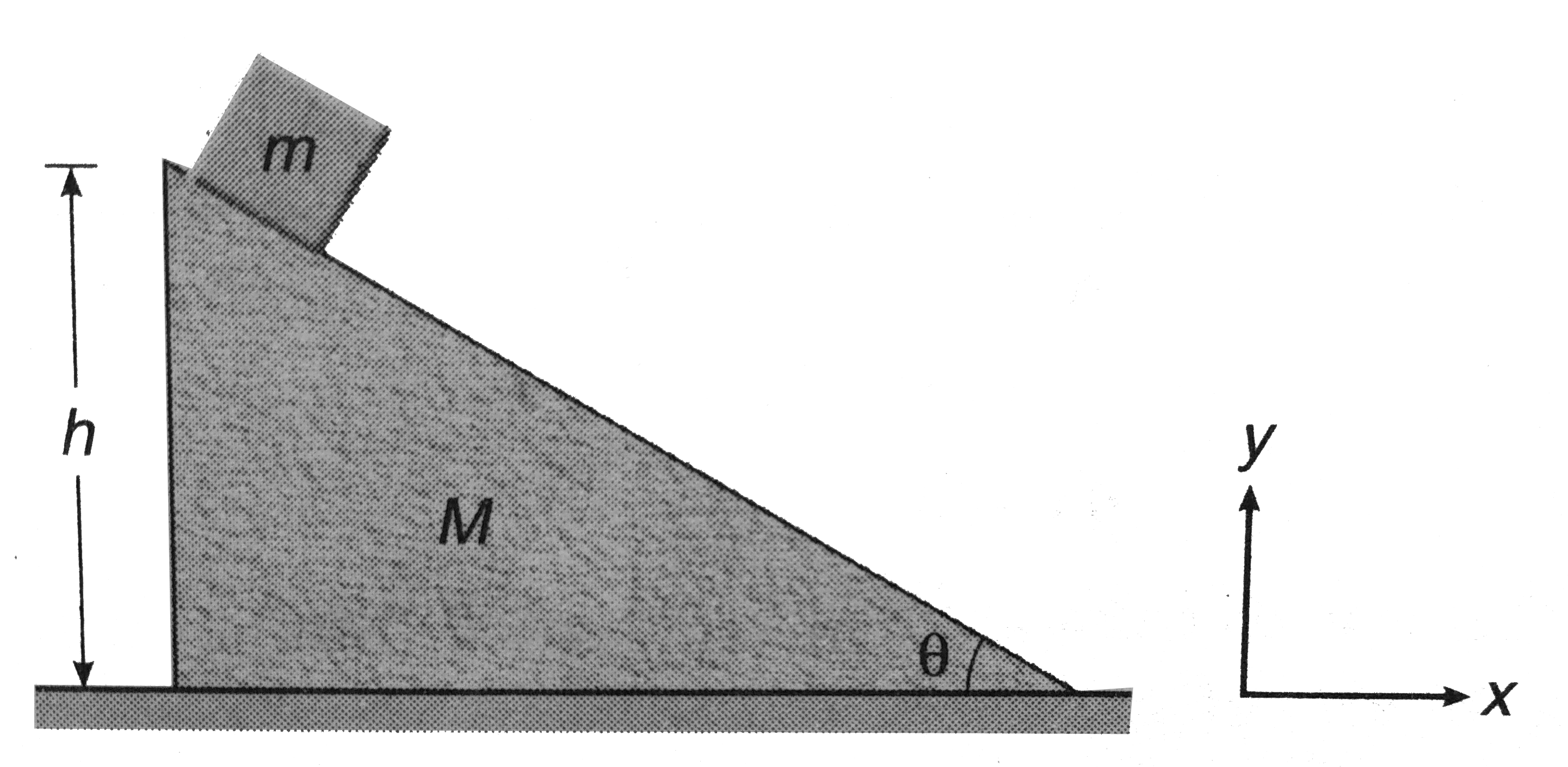
View SolutionA block of mass m is released from the top of a wedge of mass M as shown in figure. Find the displacement of wedges on the horizontal ground when the block reaches the bottom of the wedges. Neglect friction everywhere.
View Solution
