A 3.0kg block slides on a frictionless horizontal surface, first moving to the left at 50m/s. It collides with a spring as it moves left, compresses the spring and is brought to rest momentarily. The body continues to be accelerated to the right by the force of compressed spring. Finally, the body moves to the right at 40m/s. The block remains in contact with the spring for 0.020s. What were the magnitude and direction of the impulse of the spring on the block? What was the spring's average force on the block?
The correct Answer is:A, B, C
To solve the problem, we need to find two things: the magnitude and direction of the impulse of the spring on the block, and the average force exerted by the spring on the block.
Step 1: Determine the Change in Velocity
The block initially moves to the left at a velocity of vi=−50m/s (negative because it is to the left). After compressing the spring, it comes to rest momentarily, and then it moves to the right at a velocity of vf=40m/s (positive because it is to the right).
Step 2: Calculate the Change in Velocity
The change in velocity (Δv) can be calculated as:
Δv=vf−vi=40m/s−(−50m/s)=40m/s+50m/s=90m/s
Step 3: Calculate the Impulse
Impulse (J) is defined as the product of mass (m) and change in velocity (Δv):
J=m⋅Δv
Given that the mass of the block is m=3.0kg:
J=3.0kg⋅90m/s=270kg m/s
The direction of the impulse is to the right (positive direction).
Step 4: Calculate the Average Force
Impulse can also be expressed in terms of average force (Favg) and the time duration (Δt) during which the force acts:
J=Favg⋅Δt
We know that Δt=0.020s. Rearranging the formula to find the average force gives us:
Favg=JΔt=270kg m/s0.020s=13500N
Thus, the average force exerted by the spring on the block is 13500N to the right.
Final Answers
1. Magnitude and Direction of Impulse: 270N s to the right.
2. Average Force of the Spring on the Block: 13500N to the right.
The block initially moves to the left at a velocity of vi=−50m/s (negative because it is to the left). After compressing the spring, it comes to rest momentarily, and then it moves to the right at a velocity of vf=40m/s (positive because it is to the right).
The change in velocity (Δv) can be calculated as:
Δv=vf−vi=40m/s−(−50m/s)=40m/s+50m/s=90m/s
Impulse (J) is defined as the product of mass (m) and change in velocity (Δv):
J=m⋅Δv
Given that the mass of the block is m=3.0kg:
J=3.0kg⋅90m/s=270kg m/s
The direction of the impulse is to the right (positive direction).
Impulse can also be expressed in terms of average force (Favg) and the time duration (Δt) during which the force acts:
J=Favg⋅Δt
We know that Δt=0.020s. Rearranging the formula to find the average force gives us:
Favg=JΔt=270kg m/s0.020s=13500N
Thus, the average force exerted by the spring on the block is 13500N to the right.
1. Magnitude and Direction of Impulse: 270N s to the right.
2. Average Force of the Spring on the Block: 13500N to the right.
Topper's Solved these Questions
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Subjective Questions
1 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Single Correct
23 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 1 Objective
42 Videos
- CENTRE OF MASS, IMPULSE AND MOMENTUMBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, IMPULSE AND MOMENTUMEXERCISE - Comprehension type questions
15 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
Similar Questions
A 16kg block moving on a frictionless horizontal surface with a velocity of 4m/s compresses an ideal spring and comes to rest. If the force constant of the spring be 100N/m, then how much is the spring commpressed ?
View SolutionA solid sphere of mass 2 kg is rolling on a frictionless horizontal surface with velocity 6m/s. It collides on the free end of an ideal spring whose other end is fixed. The maximum compression produced in the spring will be
(Force constant of the spring = 36 N/m)
View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA block of mass 2.0 kg is moving on a frictionless horizontal surface with a velocity of 1.0 m/s figure towards another block of equal mass kept at rest. The spring constant of the spring fixed at one end is 100 N/m. Find the maximum compression of the spring.

View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
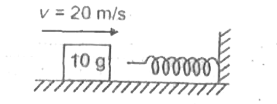
View SolutionA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
View SolutionA block of 200 g mass is dropped from a height of 2 m on to a spring and compress the spring to a distance of 50 cm. The force constant of the spring is
View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.
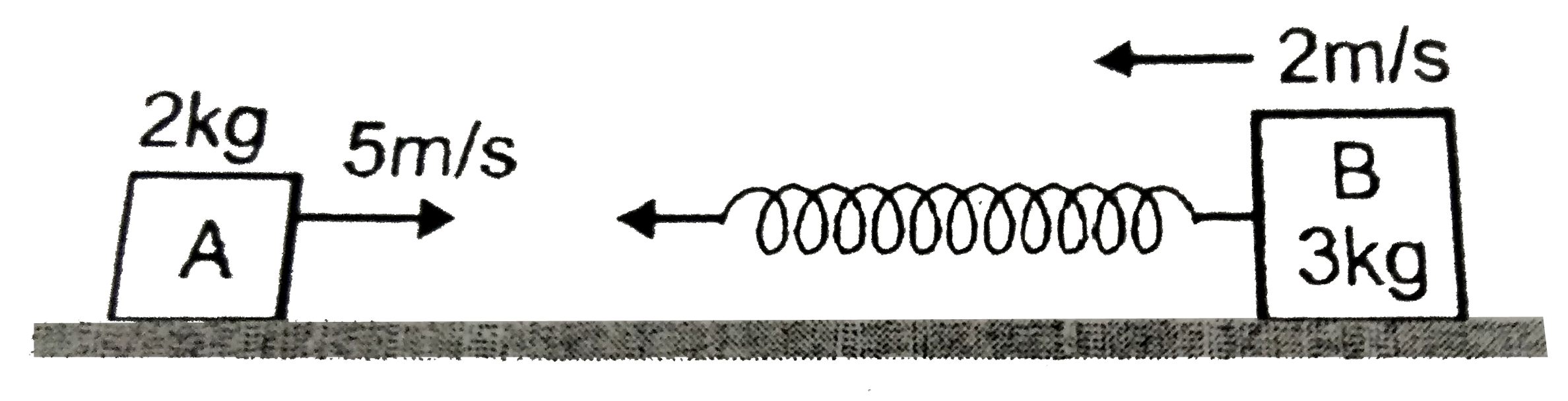
When the blocks are yet to attain their final velocities, in this situation at any instant when block A is moving with a velocity 4ˆim/s , velocity of block B will then be :
View SolutionA body of mass 0.1 g moving with a velocity of 10 m/s hits a spring (fixed at the other end) of force constant 1000 N/m and comes to rest after compressing the spring. The compression of the spring is
View SolutionIn figure, a block A of mass 2kg is moving to the right with a speed 5m/s on a horizontal frictionless surface. Another block B of mass 3kg a massless spring of spring constant 222N/m attached to it, is moving to the left on the same surface and with a speed 2m/s . Let us take the direction to the right as the positive X− direction. At some instant, block A collides with the spring attached to block B. At some other instant , the spring has maximum compression and then, finally, blocks move with their final velocities. Assuming that (i) the spring force is conservative and so there is no conversion of kinetic energy to internal energy and (ii), no sound is made when block A hits the spring, answer the following questions.

Maximum compression of the spring in the collision will be nearly
View Solution
