Particles of masses 1g, 2g, 3g ….100g are kept at the marks 1cm, 2cm, 3cm …., 100 cm respectively on a metre scale. Find the moment of inertia of the system of particles about a perpendicular bisector of the metre scale.
0.43kgm2
0.53kgm2
1.43kgm2
0.33kgm2
To find the moment of inertia of the system of particles about a perpendicular bisector of the meter scale, we can follow these steps:
Step 1: Understand the setup
We have particles of masses from 1g to 100g placed at positions from 1cm to 100cm on a meter scale. The perpendicular bisector of the meter scale is at the 50cm mark.
Step 2: Identify the moment of inertia formula
The moment of inertia I for a system of particles is given by the formula:
I=∑mir2i
where mi is the mass of the particle and ri is the distance from the axis of rotation (the perpendicular bisector in this case).
Step 3: Calculate distances from the bisector
The distance ri for each mass can be calculated as follows:
- For the mass at 1cm: r1=50−1=49 cm
- For the mass at 2cm: r2=50−2=48 cm
- ...
- For the mass at 49cm: r49=50−49=1 cm
- For the mass at 50cm: r50=50−50=0 cm
- For the mass at 51cm: r51=51−50=1 cm
- ...
- For the mass at 100cm: r100=100−50=50 cm
Step 4: Pairing the masses
Notice that for each mass mi at position i and mass m100−i at position 100−i, the distances are equal. Thus, we can pair the masses:
- Mass at 1g (1cm) and mass at 100g (100cm) both have a distance of 49cm from the bisector.
- Mass at 2g (2cm) and mass at 99g (99cm) both have a distance of 48cm from the bisector.
- This pattern continues until we reach the center.
Step 5: Write the moment of inertia expression
We can express the moment of inertia as:
I=100∑i=1mir2i
This can be simplified by recognizing the symmetry and pairing:
I=100×(492+482+472+...+12+02)
Step 6: Calculate the sum of squares
The sum of squares formula is:
n∑i=1i2=n(n+1)(2n+1)6
For n=49:
49∑i=1i2=49⋅50⋅996
Step 7: Substitute and calculate
Now substitute back into the moment of inertia formula:
I=100×(502+49∑i=1i2)
Calculating the sum:
49∑i=1i2=49⋅50⋅996=40425
Thus,
I=100×(502+40425)=100×(2500+40425)=100×42925=4292500 g cm2
Step 8: Convert to SI units
To convert to SI units (kg m²):
I=429250010000=429.25 kg m2
Final Answer
Thus, the moment of inertia of the system about the perpendicular bisector is approximately:
I≈0.42925 kg m2≈0.43 kg m2
We have particles of masses from 1g to 100g placed at positions from 1cm to 100cm on a meter scale. The perpendicular bisector of the meter scale is at the 50cm mark.
The moment of inertia I for a system of particles is given by the formula:
I=∑mir2i
where mi is the mass of the particle and ri is the distance from the axis of rotation (the perpendicular bisector in this case).
The distance ri for each mass can be calculated as follows:
- For the mass at 1cm: r1=50−1=49 cm
- For the mass at 2cm: r2=50−2=48 cm
- ...
- For the mass at 49cm: r49=50−49=1 cm
- For the mass at 50cm: r50=50−50=0 cm
- For the mass at 51cm: r51=51−50=1 cm
- ...
- For the mass at 100cm: r100=100−50=50 cm
Notice that for each mass mi at position i and mass m100−i at position 100−i, the distances are equal. Thus, we can pair the masses:
- Mass at 1g (1cm) and mass at 100g (100cm) both have a distance of 49cm from the bisector.
- Mass at 2g (2cm) and mass at 99g (99cm) both have a distance of 48cm from the bisector.
- This pattern continues until we reach the center.
We can express the moment of inertia as:
I=100∑i=1mir2i
This can be simplified by recognizing the symmetry and pairing:
I=100×(492+482+472+...+12+02)
The sum of squares formula is:
n∑i=1i2=n(n+1)(2n+1)6
For n=49:
49∑i=1i2=49⋅50⋅996
Now substitute back into the moment of inertia formula:
I=100×(502+49∑i=1i2)
Calculating the sum:
49∑i=1i2=49⋅50⋅996=40425
Thus,
I=100×(502+40425)=100×(2500+40425)=100×42925=4292500 g cm2
To convert to SI units (kg m²):
I=429250010000=429.25 kg m2
Thus, the moment of inertia of the system about the perpendicular bisector is approximately:
I≈0.42925 kg m2≈0.43 kg m2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.2
Explore 4 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Exercise 12.3
Explore 4 Videos
- ROTATIONAL MECHANICSBook:DC PANDEY ENGLISHChapter:ROTATIONAL MECHANICSExercise:Solved Example
Explore 1 Video
- ROTATIONBook:DC PANDEY ENGLISHChapter:ROTATIONExercise:(C) Chapter Exercises
Explore 39 Videos
- ROTATIONAL MOTIONBook:DC PANDEY ENGLISHChapter:ROTATIONAL MOTIONExercise:Integer Type Questions
Explore 17 Videos
Similar Questions
Two masses of 3kg and 5kg are placed at 20 cm and 70cm marks respectively on a light wooden meter scale. The M.I. of the system about an axis passign through 100cm mark and perpendicular to the meter scale is
View SolutionThree particles, each of mass 200 g are kept at the corners of an equilateral triangle of side 10 cm. Find the moment of inertia of the system about an axis
a. joining two of the particles
b. passing through one of the particle perpendicular to the plane of the particles.
View Solution
Knowledge Check
If the centre of gravity of a metre scale of mass 80g lies at the 45 cm mark, then which one of the following diagrams will show the balanced position of the scale.
A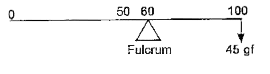 B
B C
C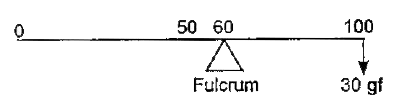 D
D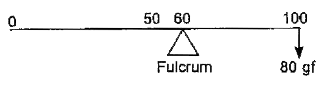
Three particles of masses 1 g, 2g and 3 g are kept at points (2cm,0), (0.6 cm), (4cm, 3cm) find moment of inertia of all three particles (in gm−cm(2)) about (a) x-axis
(b). Y-axis
(c). Z-axis.
View SolutionThe coordinates of the centre of mass of a system of three particles of mass 1g,2g and 3g are (2,2,2). Where should a fourth particle of mass 4 g be positioned so that the centre of mass of the four particle system is at the origin of the three-dimensional coordinate system ?
View SolutionA particle of mass 100 g is kept on the surface of a uniform sphere of mass 10 kg and radius 10 cm. Find the work to be done against the gravitational force between them to take the particle away from the sphere.
View SolutionTwo discs of same mass and same thickness have densities as 17g/cm3 and 51g/cm3. The ratio of their moment of inertia about their central axes is
View SolutionA uniform metre scale can be balanced at the 70.0 cm mark when a mass of 0.05 kg is hung from the 94.0 cm mark.
Find the mass of the metre scale.
View SolutionTwo immiscible of densities 2.5g/cm3 and 0.8g/cm3 are taken in the ratio of their masses as 2:3 respectively find the average density of the liquid conbination.
View SolutionA cork has a volume 25cm3 . The density of cork is 0.25gcm−3 . Find the mass of the cork.
View Solution
