The angular velocity of a gar is controlled according to ω=12−3t2 where ω in radian per second, is positive in the clockwise sense and t is the time in seconds. Find the net angular displacement △θ from the time t=0 to t=3s. Also, find the number of revolutions N through which the gear turns during the 3s.
To solve the problem, we need to find the net angular displacement Δθ from t=0 to t=3 seconds and the number of revolutions N the gear makes during this time.
Step 1: Write down the expression for angular velocity
The angular velocity ω is given by:
ω=12−3t2
Step 2: Find the angular displacement
The angular displacement Δθ can be found by integrating the angular velocity over the time interval from t=0 to t=3:
Δθ=∫30ωdt=∫30(12−3t2)dt
Step 3: Perform the integration
We can split the integral:
Δθ=∫3012dt−∫303t2dt
Calculating the first integral:
∫3012dt=12t∣∣∣30=12×3−12×0=36
Calculating the second integral:
∫303t2dt=3⋅t33∣∣∣30=t3∣∣∣30=33−03=27
Step 4: Combine the results
Now we can combine the results of the integrals:
Δθ=36−27=9 radians
Step 5: Find the number of revolutions
To find the number of revolutions N, we use the formula:
N=Δθ2π
Substituting the value of Δθ:
N=92π
Using π≈3.142:
N≈92×3.142≈96.284≈1.43
Final Answers
- The net angular displacement Δθ is 9 radians.
- The number of revolutions N is approximately 1.43.
The angular velocity ω is given by:
ω=12−3t2
The angular displacement Δθ can be found by integrating the angular velocity over the time interval from t=0 to t=3:
Δθ=∫30ωdt=∫30(12−3t2)dt
We can split the integral:
Δθ=∫3012dt−∫303t2dt
∫3012dt=12t∣∣∣30=12×3−12×0=36
∫303t2dt=3⋅t33∣∣∣30=t3∣∣∣30=33−03=27
Now we can combine the results of the integrals:
Δθ=36−27=9 radians
To find the number of revolutions N, we use the formula:
N=Δθ2π
Substituting the value of Δθ:
N=92π
Using π≈3.142:
N≈92×3.142≈96.284≈1.43
- The net angular displacement Δθ is 9 radians.
- The number of revolutions N is approximately 1.43.
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.5
7 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.6
4 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.3
4 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The angular velocity of a particle is given by ω=1.5t−3t∘+2, Find the time when its angular acceleration becomes zero.
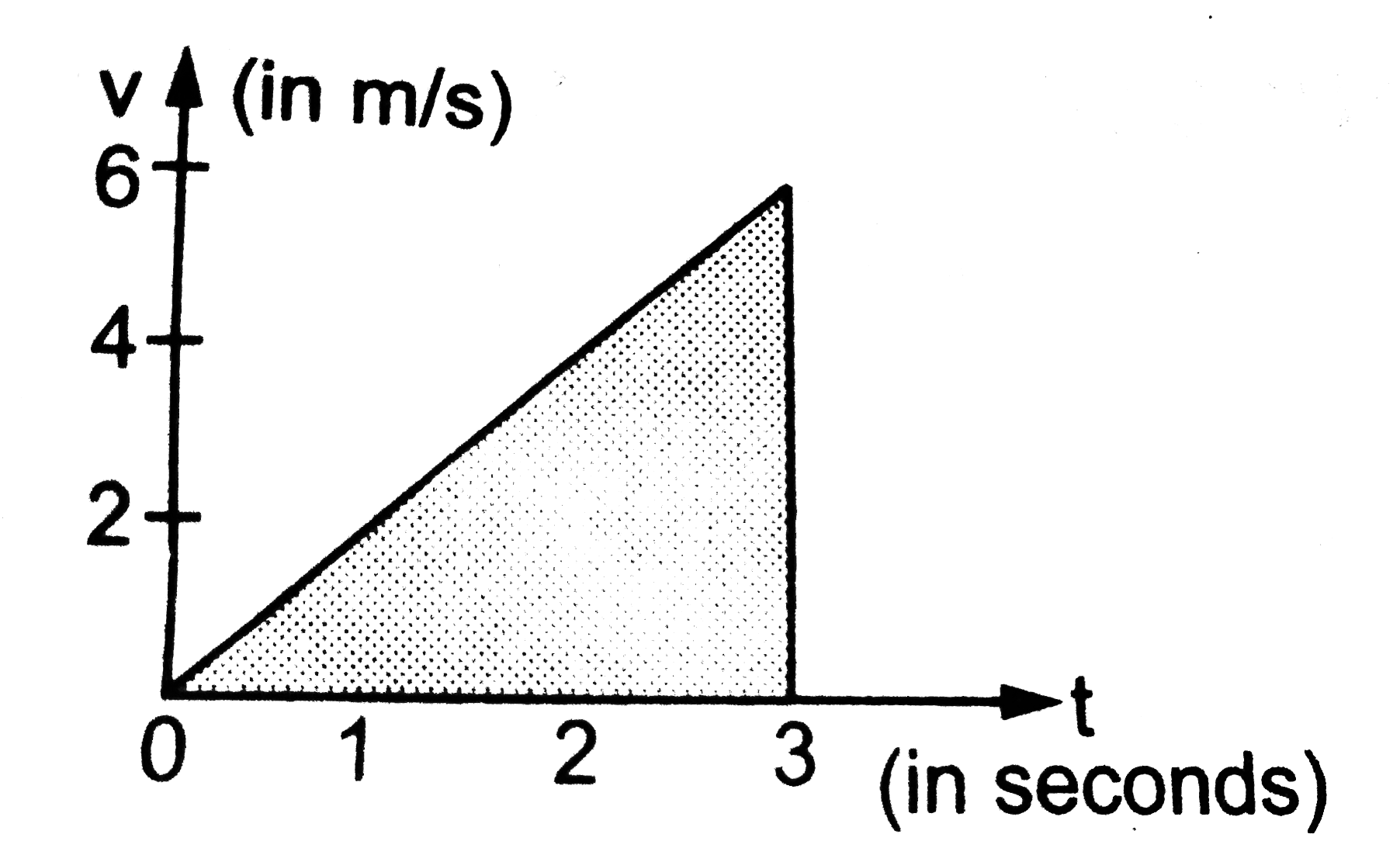
View SolutionFigure shows the speed versus time graph for a particle. Find the distance travelled by the particle during the time t=0 to t=3s.
View SolutionThe velocity of a particle is given by v=(2t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=2 second.
View SolutionThe voltage supplied to a circuit is given by V=V0t32, where t is time in second. Find the rms value of voltage for the period, t=0 to t=1s.
View SolutionAn object moves along x-axis such that its position varies with time according to the relation x=50t−5t2
Here, x is in meters and time is in seconds. Find the displacement and distance travelled for the time interval t = 0 to t = 6 s.
View SolutionA particle is acted upon by a force given by F=(12t−3t2)N, where is in seconds. Find the change in momenum of that particle from t=1 to t=3 sec.
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View SolutionThe angular displacement of a particle is given by θ=t4+t3+t2+1 where ‘t’ is time in seconds. Its angular velocity after 2 sec is
View SolutionThe velocity of a particle is given by v=(4t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=1 second.
View SolutionThe position of a particle is expressed as →r=(4t2ˆi+2tˆj) m, where t is time in second. Find the velocity o the particle at t = 3 s
View Solution
