The voltage supplied to a circuit is given by V=V0t32, where t is time in second. Find the rms value of voltage for the period, t=0 to t=1s.
To find the RMS (Root Mean Square) value of the voltage given by the equation V=V0t3/2 from t=0 to t=1 second, we can follow these steps:
Step 1: Understand the RMS Formula
The RMS value of a function over a time interval is given by the formula:
VRMS=√1T∫T0V2dt
where T is the time period over which we are calculating the RMS value.
Step 2: Substitute the Voltage Function
In our case, the voltage function is V=V0t3/2. Therefore, we need to calculate V2:
V2=(V0t3/2)2=V20t3
Step 3: Set Up the Integral
Now, we substitute V2 into the RMS formula:
VRMS=√11∫10V20t3dt
This simplifies to:
VRMS=√∫10V20t3dt
Step 4: Calculate the Integral
We need to evaluate the integral ∫10t3dt:
∫t3dt=t44
Now we evaluate this from 0 to 1:
∫10t3dt=(t44)10=144−044=14
Step 5: Substitute Back into the RMS Formula
Now we substitute the result of the integral back into the RMS formula:
VRMS=√V20⋅14=√V204=V02
Final Answer
Thus, the RMS value of the voltage for the period t=0 to t=1 second is:
VRMS=V02
The RMS value of a function over a time interval is given by the formula:
VRMS=√1T∫T0V2dt
where T is the time period over which we are calculating the RMS value.
In our case, the voltage function is V=V0t3/2. Therefore, we need to calculate V2:
V2=(V0t3/2)2=V20t3
Now, we substitute V2 into the RMS formula:
VRMS=√11∫10V20t3dt
This simplifies to:
VRMS=√∫10V20t3dt
We need to evaluate the integral ∫10t3dt:
∫t3dt=t44
Now we evaluate this from 0 to 1:
∫10t3dt=(t44)10=144−044=14
Now we substitute the result of the integral back into the RMS formula:
VRMS=√V20⋅14=√V204=V02
Thus, the RMS value of the voltage for the period t=0 to t=1 second is:
VRMS=V02
Similar Questions
The electric current in a circuit is given by
i=3t
Here, t is in second and I in ampere. The rms current for the period to=0 to t=1 s is
View SolutionThe velocity of a particle is given by v=(4t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=1 second.
View SolutionThe velocity of a particle is given by v=(2t2−4t+3)m/s where t is time in seconds. Find its acceleration at t=2 second.
View SolutionThe current in a discharging LR circuit is given by I=i0(tτ) where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionThe current in a discharging LR circuit is given by I=i0e−tτ where τ is the time constant of the circuit. Calculate the rms current for the period t=0 to t=τ.
View SolutionA particle moves in a circle of radius 20 cm. Its linear speed is given by v=(3t2+5t) where t is in second and v is in m/s. Find the resultant acceleration at t = 1s.
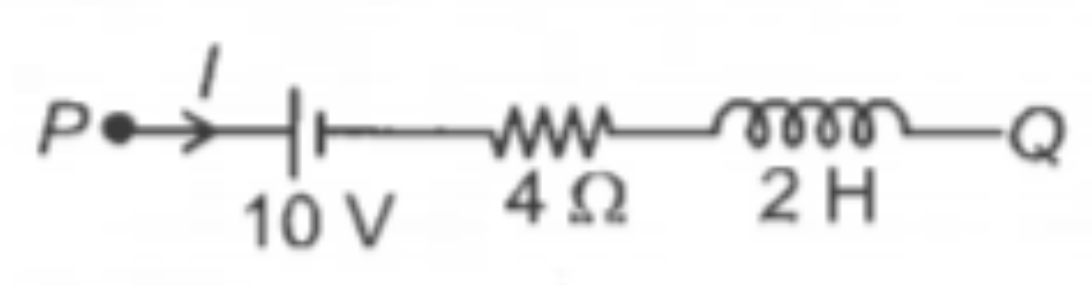
View SolutionIn the given branch PQ of a circuit, a current / = (2+ + 3) A is flowing where t is time in second. Then the value of potential difference (Vp−Vq) at t = 2 s will be
View SolutionThe speed(v) of a particle moving along a straight line is given by v=(t2+3t−4 where v is in m/s and t in seconds. Find time t at which the particle will momentarily come to rest.
View SolutionA particle moves in circle of radius 1.0 cm at a speed given by v=2.0 t where v is in cm/s and t in seconeds. A. find the radia accelerationof the particle at t=1 s. b. Findthe tangential acceleration at t=1s. c.Find the magnitude of the aceleration at t=1s.
View SolutionGiven figure is the part of some circuit. Charge on the capacitor in the circuit is given by q=3(3−e−t), (coulomb) where t is time in seconds.
Let VA, VB and VC be the potentials of points A, B and C, respectively. At t=0 if VA=5V and a constant current i0=1Amp flows through R=1Ω, then find the VP (in volt)
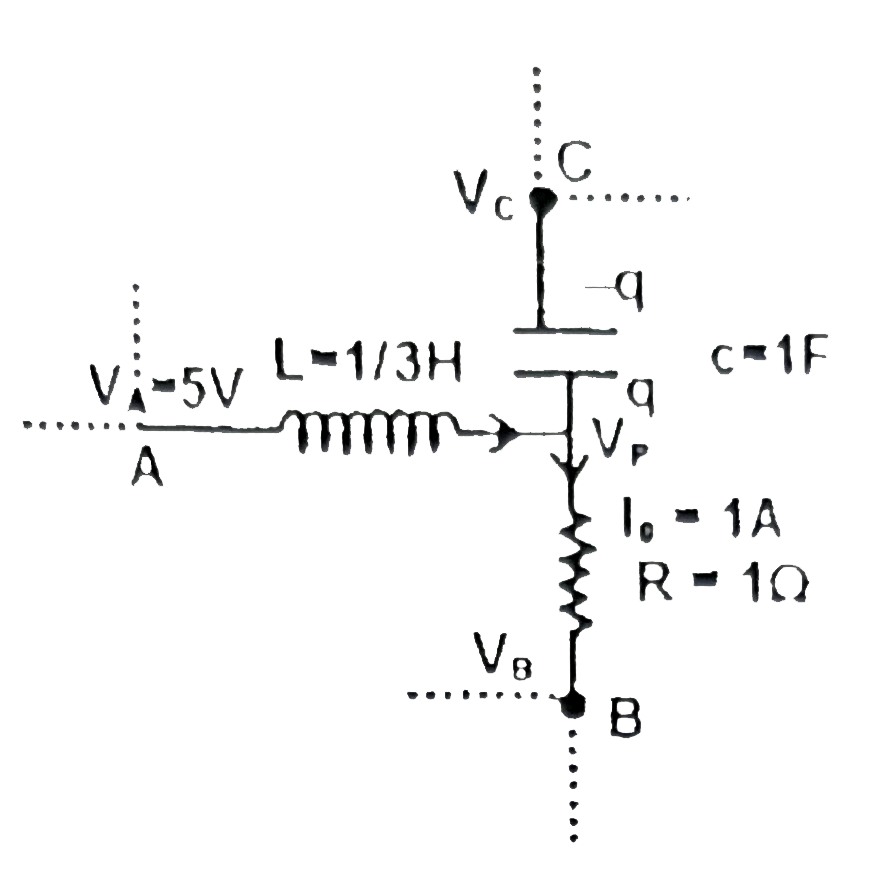
View Solution
