In the same figure. If v and ω both are constant, then find linear acceleration of point M,N,R and S in terms of R,ω,ˆi and ˆj where R is the radius disc.
To solve the problem of finding the linear acceleration of points M, N, R, and S on a rotating disk with constant linear velocity v and angular velocity ω, we can follow these steps:
1. Understanding the Motion:
The disk is undergoing both translational and rotational motion. Since both v (linear velocity) and ω (angular velocity) are constant, we can analyze the motion in two parts: the translational motion of the center of mass and the rotational motion about the center of mass.
Hint: Identify the types of motion involved (translational and rotational).
2. Acceleration of the Center of Mass:
Since the linear velocity v is constant, the acceleration of the center of mass of the disk with respect to the ground is zero. This means that there is no net external force acting on the disk in the direction of its motion.
Hint: Recall that constant velocity implies zero acceleration.
3. Acceleration of Points on the Disk:
To find the acceleration of points M, N, R, and S, we need to consider their motion relative to the center of mass. The acceleration of any point on the disk can be expressed as the sum of the centripetal acceleration and tangential acceleration.
4. Centripetal Acceleration:
The centripetal acceleration ac for a point on the disk is given by the formula:
ac=v2R
where R is the radius of the disk. Since v=ωR, we can substitute this into the centripetal acceleration formula:
ac=(ωR)2R=ω2R
Hint: Remember that centripetal acceleration is directed towards the center of the circular path.
5. Tangential Acceleration:
Since both v and ω are constant, the tangential acceleration at is zero:
at=0
Hint: Constant angular velocity means no change in speed along the circular path.
6. Total Acceleration:
The total linear acceleration a of any point on the disk (M, N, R, or S) is purely centripetal, as the tangential component is zero:
a=ac+at=ω2R+0=ω2R
Hint: Combine the components of acceleration to find the total acceleration.
7. Direction of Acceleration:
The direction of the acceleration for points M, N, R, and S will be directed towards the center of the disk, as it is centripetal.
Final Result:
The linear acceleration of points M, N, R, and S in terms of R, ω, ^i, and ^j is:
Acceleration=ω2R^r
where ^r is the unit vector pointing towards the center of the disk from the respective points.
The disk is undergoing both translational and rotational motion. Since both v (linear velocity) and ω (angular velocity) are constant, we can analyze the motion in two parts: the translational motion of the center of mass and the rotational motion about the center of mass.
Since the linear velocity v is constant, the acceleration of the center of mass of the disk with respect to the ground is zero. This means that there is no net external force acting on the disk in the direction of its motion.
To find the acceleration of points M, N, R, and S, we need to consider their motion relative to the center of mass. The acceleration of any point on the disk can be expressed as the sum of the centripetal acceleration and tangential acceleration.
The centripetal acceleration ac for a point on the disk is given by the formula:
ac=v2R
where R is the radius of the disk. Since v=ωR, we can substitute this into the centripetal acceleration formula:
ac=(ωR)2R=ω2R
Since both v and ω are constant, the tangential acceleration at is zero:
at=0
The total linear acceleration a of any point on the disk (M, N, R, or S) is purely centripetal, as the tangential component is zero:
a=ac+at=ω2R+0=ω2R
The direction of the acceleration for points M, N, R, and S will be directed towards the center of the disk, as it is centripetal.
The linear acceleration of points M, N, R, and S in terms of R, ω, ^i, and ^j is:
Acceleration=ω2R^r
where ^r is the unit vector pointing towards the center of the disk from the respective points.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.83videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.92videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercise 12.64videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
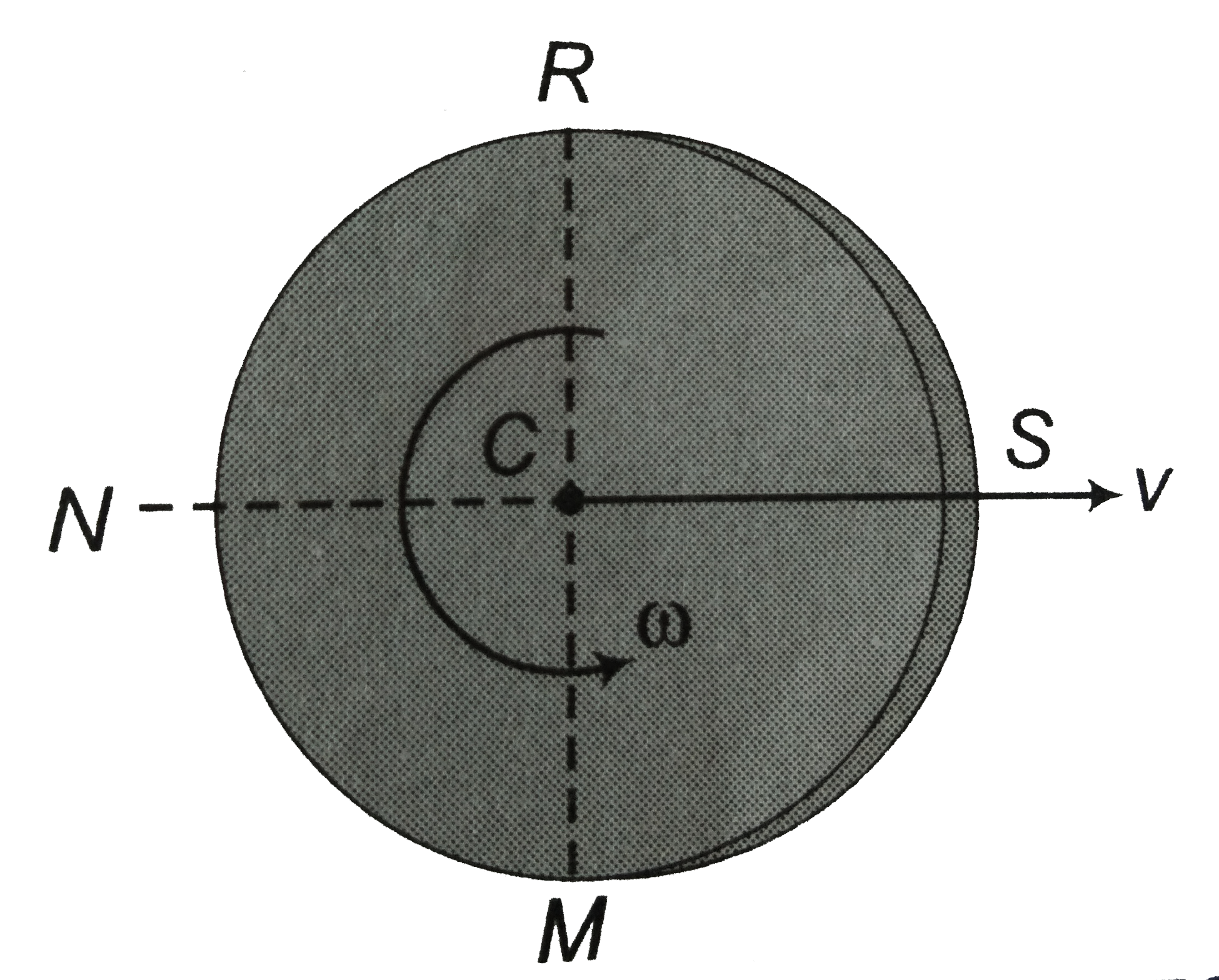
In the figure shown omega = v/2R in terms of i and j find the linear velocities of particles M,N,R and S .View Solution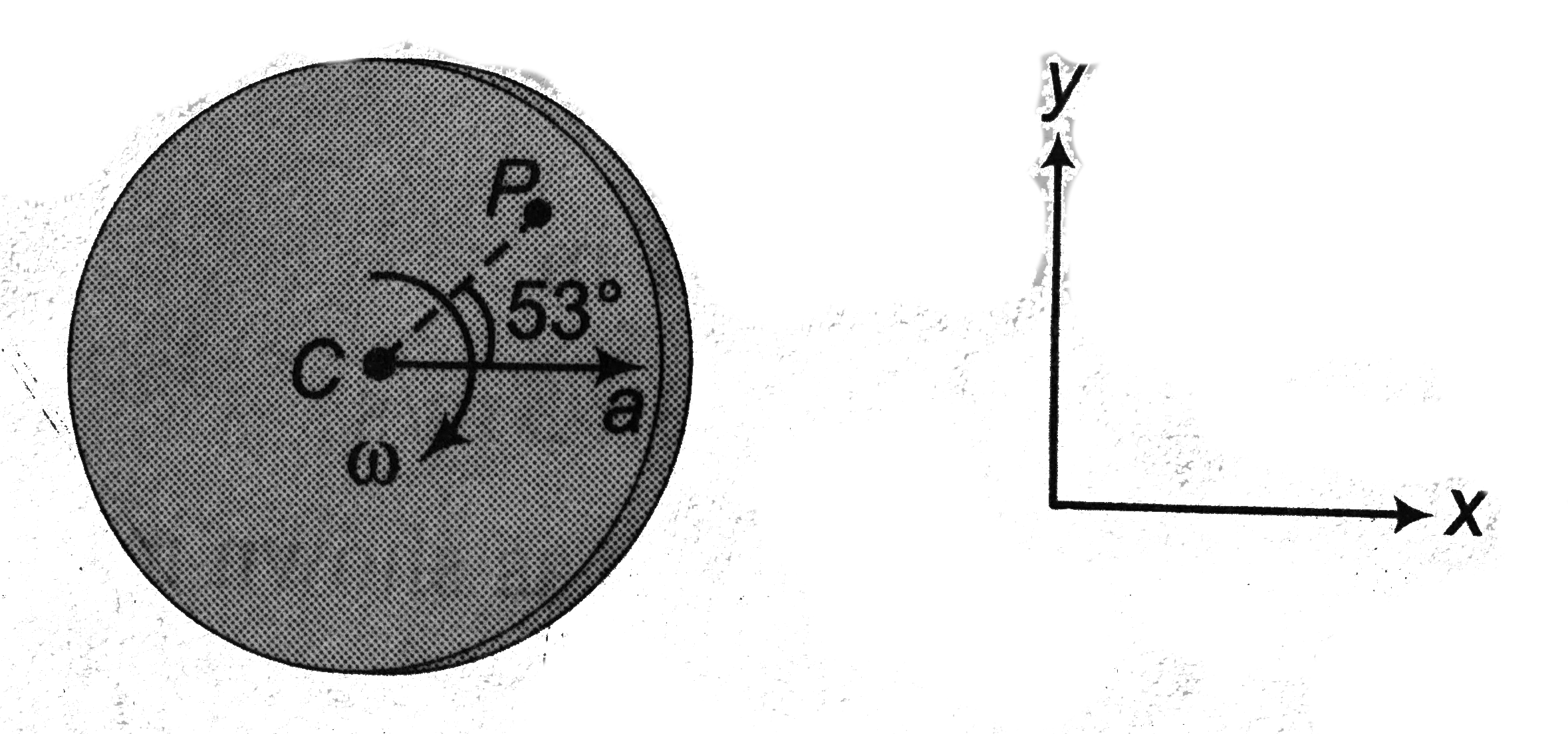
In the shown figure,
a=2m/s2,ω=(2t)rods−1 and CP=1m
In terms of ˆi and ˆj, find linear acceleration of the particle at P at P at t=1 sView Solution
A ring of radius R rolls on a horizontal surface with constant acceleration a of the centre of mass as shown in figure. If ω is the instantaneous angular velocity of the ring. Then the net acceleration of the point of contact of the ring with gound isView SolutionChoose the correct option:
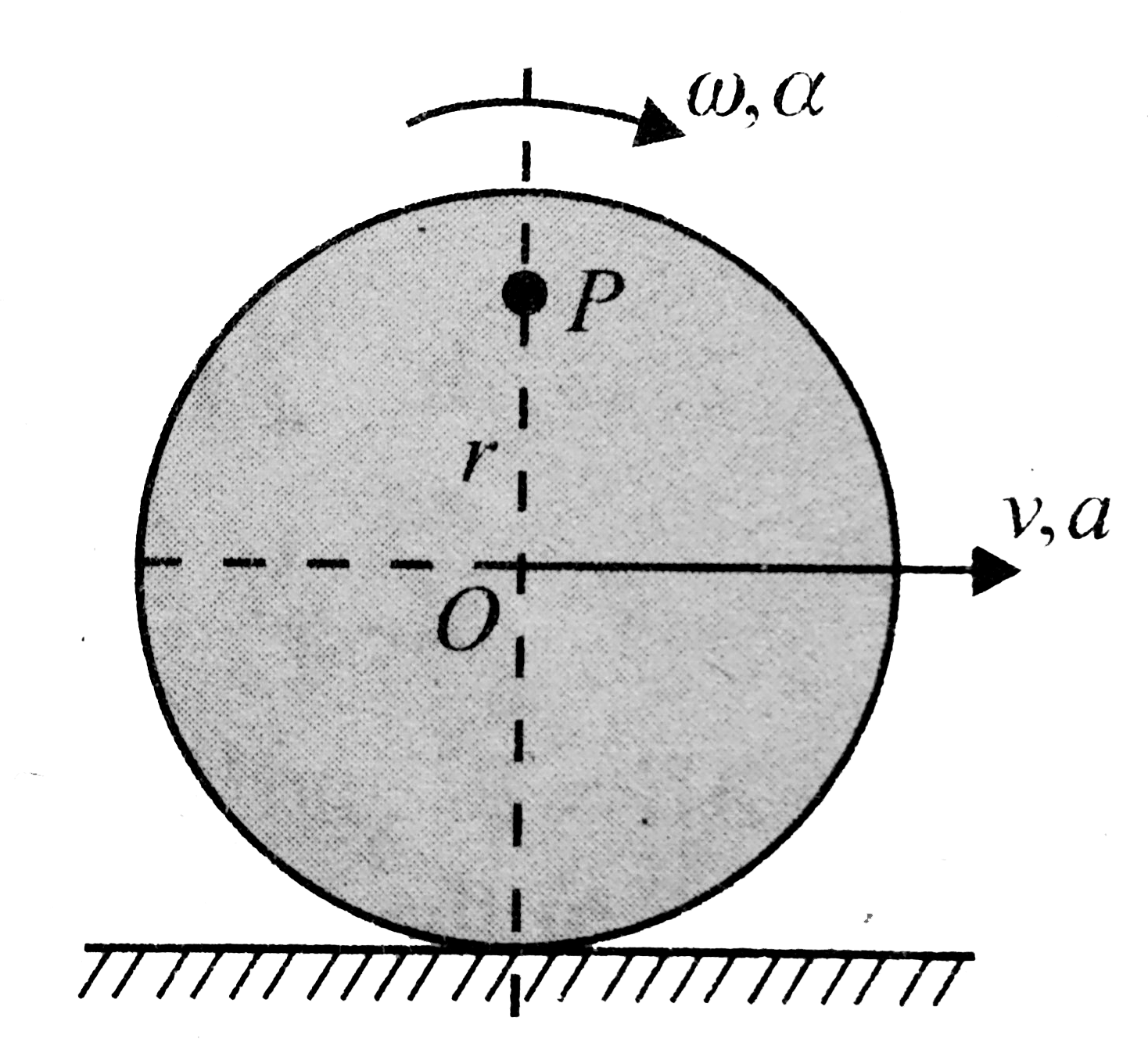
A disc of radius R rolls on a horizontal ground with linear acceleration a and angular acceleration α as shown in Fig. The magnitude of acceleration of point P as shown in the figure at an instant when its linear velocity is v and angular velocity is ω will be a
 View Solution
View SolutionSolve the following linear inequation in R: 4x−2<8, when x∈R
View SolutionSolve the following linear inequation in R: 4x−2<8, when x∈N
View SolutionSolve the following linear inequation in R: 12x<50, when x∈R
View SolutionSolve the following linear inequation in R: 12x<50, when x∈N
View Solution
In the figure shown υ=2m/s ω=5rad/s and CP=1m
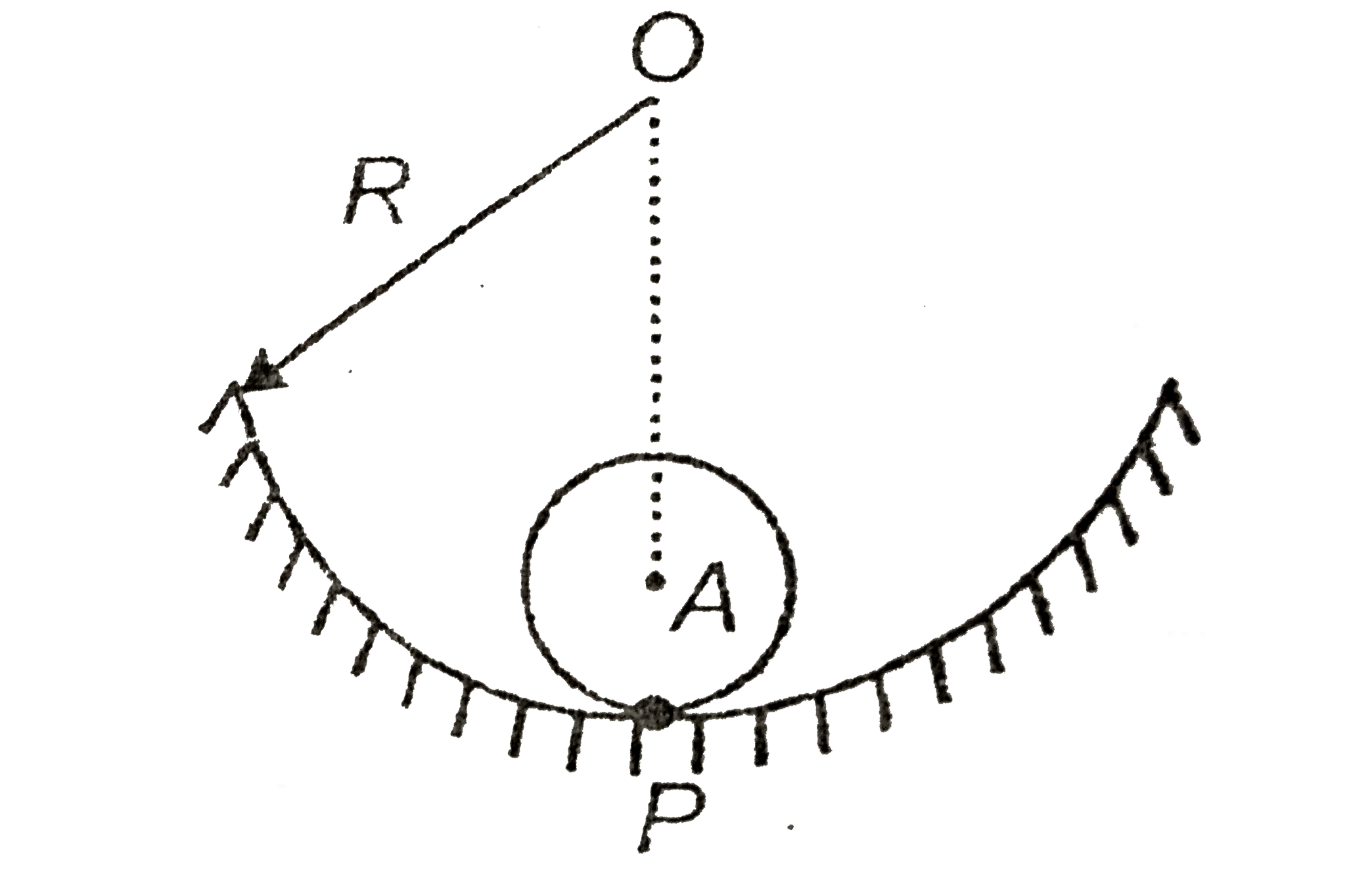
In terms of ˆi and ˆj find linear velocity of particle P.View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
 View Solution
View Solution

