Moment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
736ML2
748ML2
1148ML2
ML212
The correct Answer is:B
I=ML212+M(L4)2=748ML2
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 1 Subjective
32 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Assertion And Reason
11 Videos
- ROTATIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View Solution
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
The moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
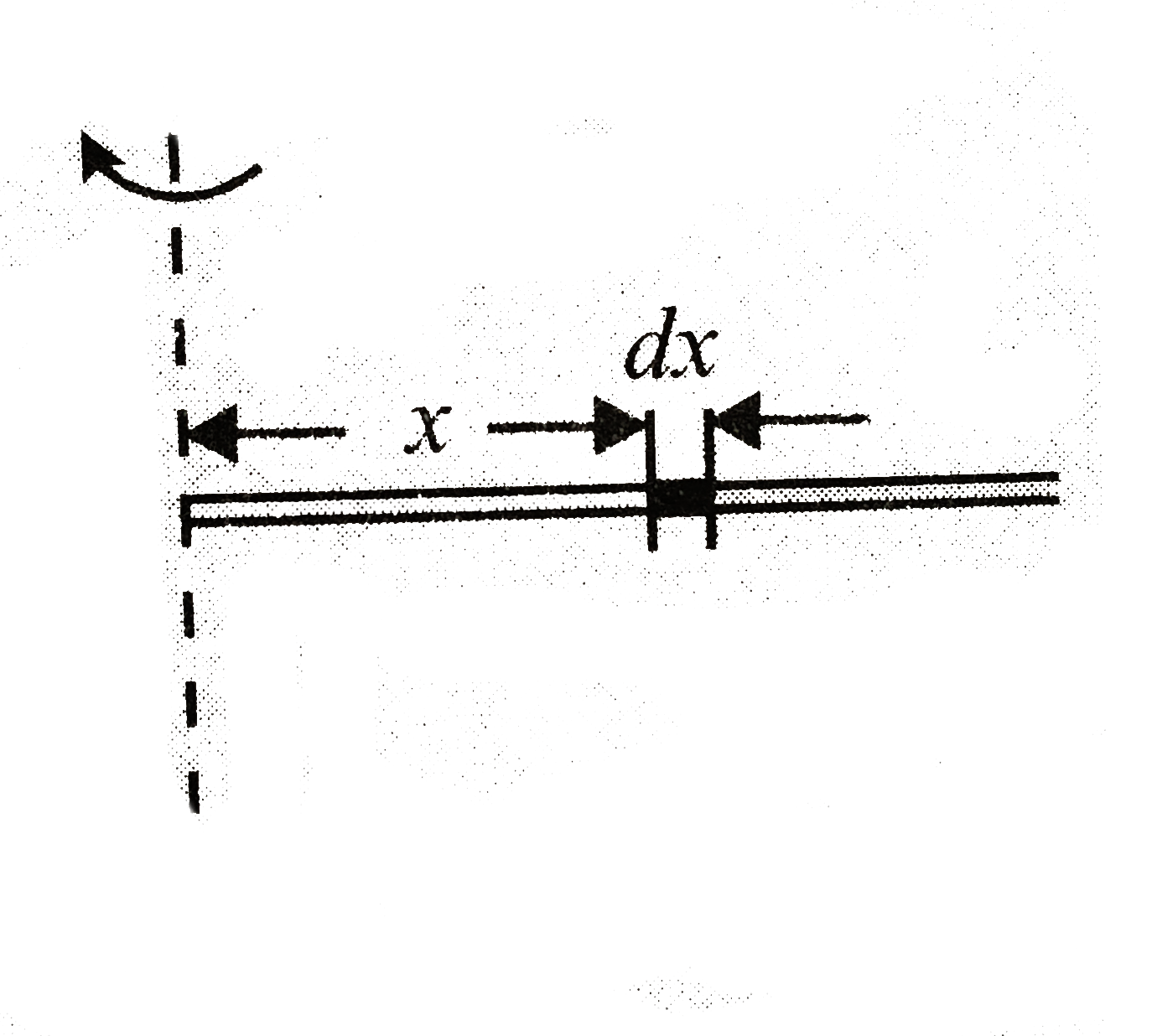
View SolutionThe moment of inertia of a thing uniform rod of length L and mass M, about axis CD (as shown in figure) is

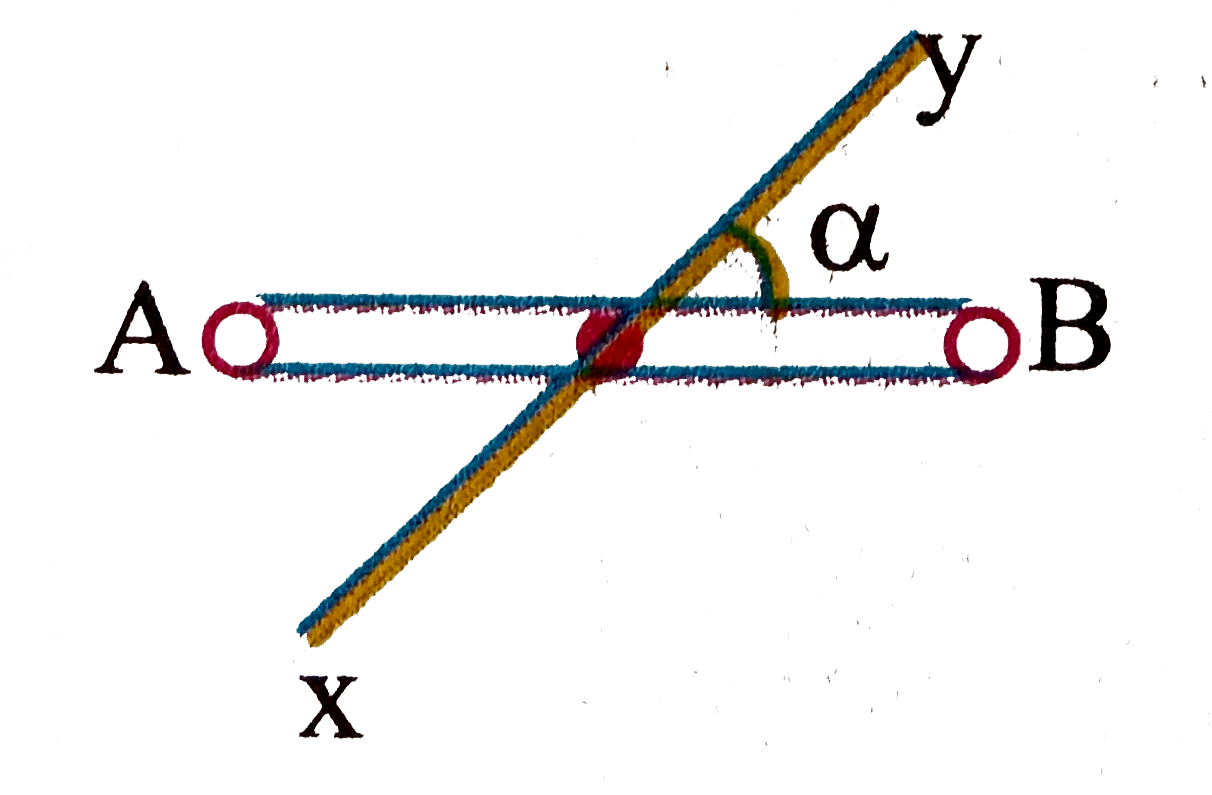
View SolutionThe moment of inertia of a uniform rod of length 2l and mass m about an axis xy passing through its centre and inclined at an enable α is
View SolutionMoment of inertia of a cylinder of mass M, length L and radius R about an axis passing through its centre and perpendicular to the axis of the cylinder is I=M(R24+L212). If such a cylinder is to be made for a given mass of a material, the ratio L/R for it to have minimum possible I is :
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View Solution
