Moment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
ml212
ml23
7ml248
ml29
The correct Answer is:C
To find the moment of inertia of a thin rod of mass m and length l about an axis passing through a point l4 from one end and perpendicular to the rod, we can follow these steps:
1. Identify the Moment of Inertia about the Center of Mass (CM):
The moment of inertia of a thin rod about its center of mass (which is at a distance l2 from either end) is given by the formula:
ICM=112ml2
2. Determine the Distance from the Center of Mass to the New Axis:
The new axis is located l4 from one end. The distance from the center of mass to this new axis can be calculated as follows:
- The distance from one end to the center of mass is l2.
- The distance from the center of mass to the new axis is:
d=l2−l4=l4
3. Apply the Parallel Axis Theorem:
The parallel axis theorem states that the moment of inertia about a new axis parallel to the one through the center of mass is given by:
I=ICM+md2
Substituting the values we have:
I=112ml2+m(l4)2
4. Calculate md2:
Now calculate md2:
md2=m(l4)2=ml216
5. Combine the Terms:
Substitute ICM and md2 into the equation:
I=112ml2+ml216
6. Find a Common Denominator:
The common denominator for 12 and 16 is 48:
- Convert 112 to 448
- Convert 116 to 348
Therefore:
I=448ml2+348ml2=748ml2
7. Final Result:
The moment of inertia of the thin rod about the specified axis is:
I=748ml2
The moment of inertia of a thin rod about its center of mass (which is at a distance l2 from either end) is given by the formula:
ICM=112ml2
The new axis is located l4 from one end. The distance from the center of mass to this new axis can be calculated as follows:
- The distance from one end to the center of mass is l2.
- The distance from the center of mass to the new axis is:
d=l2−l4=l4
The parallel axis theorem states that the moment of inertia about a new axis parallel to the one through the center of mass is given by:
I=ICM+md2
Substituting the values we have:
I=112ml2+m(l4)2
Now calculate md2:
md2=m(l4)2=ml216
Substitute ICM and md2 into the equation:
I=112ml2+ml216
The common denominator for 12 and 16 is 48:
- Convert 112 to 448
- Convert 116 to 348
I=448ml2+348ml2=748ml2
The moment of inertia of the thin rod about the specified axis is:
I=748ml2
Similar Questions
The moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View SolutionCalculate the moment of inertia of a uniform rod of mass M and length l about an axis passing through an end and perpendicular to the rod. The rod can be divided into a number of mass elements along the length of the rod.
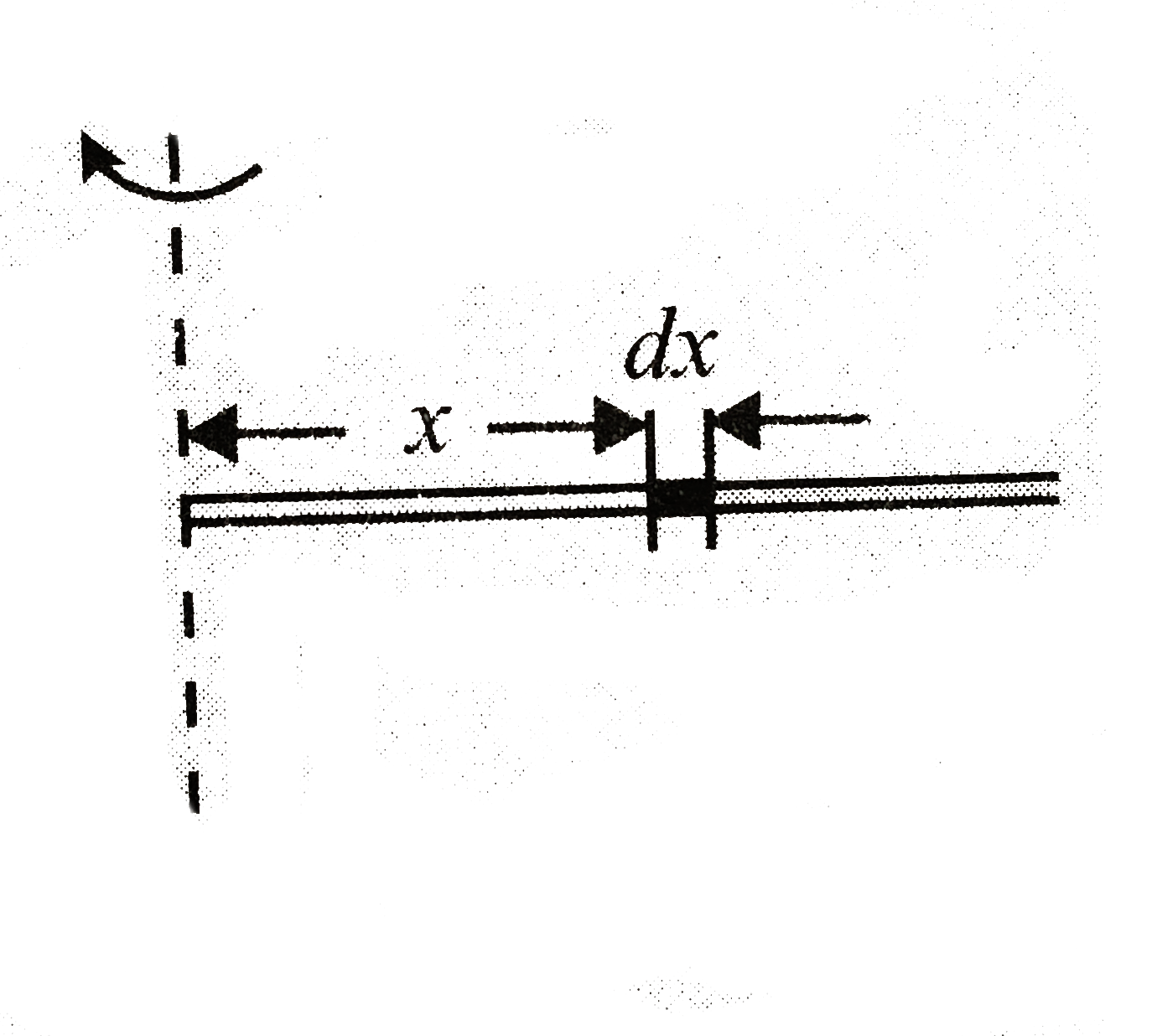
View Solution
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
Moment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View SolutionMoment of inertia of a uniform rod of length L and mass M, about an axis passing through L/4 from one end and perpendicular to its length is
View Solutionfind the radius of gyration of a rod of mass m and length 2l about an axis passing through one of its ends and perpendicular to its length.
View SolutionThe moment of inertia of a uniform thin rod of length L and mass M about an axis passing through a point at a distance of L/3 from one of its ends and perpendicular to the rod is
View SolutionThe moment of inertia of a uniform thin rod of mass m and length L about two axis PQ and RS passing through centre of rod C and in the plane of the rod are IPQ and IRS respectively. Then IPQ+IRS is equal to
View SolutionThe radius of gyration of a uniform rod of length l , about an axis passing through a point l8away form the centre of the rod , and perpendicular to it is:
View SolutionThe radius of gyration of a uniform rod of length l , about an axis passing through a point l8away form the centre of the rod , and perpendicular to it is:
View Solution