In the above problem, if any one point mass is removed then what is gravitational potential and magnitude of filed strength at centre?
The correct Answer is:A, B, D
To solve the problem of determining the gravitational potential and the magnitude of the gravitational field strength at the center of a pentagon when one point mass is removed, we can follow these steps:
1. Understanding the Configuration:
- We have a regular pentagon with 5 point masses, each of mass m, located at the vertices. The distance from the center of the pentagon to each vertex is A.
2. Removing One Mass:
- When one mass (let's say mass at vertex E) is removed, we are left with 4 masses (at vertices A, B, C, and D).
3. Gravitational Potential Calculation:
- The gravitational potential V due to a point mass m at a distance r is given by:
V=−Gmr
- For the remaining 4 masses, the potential at the center (which is equidistant from all remaining masses) will be:
Vtotal=VA+VB+VC+VD=−GmA−GmA−GmA−GmA=−4GmA
4. Gravitational Field Strength Calculation:
- The gravitational field strength E at a point due to a mass is given by:
E=−dVdr
- The gravitational field strength due to a single mass m at a distance A is:
E=GmA2
- Since we have 4 masses contributing to the field strength at the center, and due to symmetry, the resultant field strength will be the vector sum of the individual field strengths. However, because of symmetry in a regular pentagon, the horizontal components of the field strengths will cancel out, leaving only the vertical components.
- Thus, the net gravitational field strength Enet at the center is:
Enet=4⋅GmA2⋅cos(θ)
- Here, θ is the angle between the line connecting the center to the vertex and the vertical axis. For a regular pentagon, this angle can be calculated, but since we are only interested in the magnitude, we can conclude that:
Enet=4GmA2
Final Answers:
- The gravitational potential at the center after removing one mass is:
V=−4GmA
- The magnitude of the gravitational field strength at the center is:
E=4GmA2
- We have a regular pentagon with 5 point masses, each of mass m, located at the vertices. The distance from the center of the pentagon to each vertex is A.
- When one mass (let's say mass at vertex E) is removed, we are left with 4 masses (at vertices A, B, C, and D).
- The gravitational potential V due to a point mass m at a distance r is given by:
V=−Gmr
- For the remaining 4 masses, the potential at the center (which is equidistant from all remaining masses) will be:
Vtotal=VA+VB+VC+VD=−GmA−GmA−GmA−GmA=−4GmA
- The gravitational field strength E at a point due to a mass is given by:
E=−dVdr
- The gravitational field strength due to a single mass m at a distance A is:
E=GmA2
- Since we have 4 masses contributing to the field strength at the center, and due to symmetry, the resultant field strength will be the vector sum of the individual field strengths. However, because of symmetry in a regular pentagon, the horizontal components of the field strengths will cancel out, leaving only the vertical components.
- Thus, the net gravitational field strength Enet at the center is:
Enet=4⋅GmA2⋅cos(θ)
- Here, θ is the angle between the line connecting the center to the vertex and the vertical axis. For a regular pentagon, this angle can be calculated, but since we are only interested in the magnitude, we can conclude that:
Enet=4GmA2
- The gravitational potential at the center after removing one mass is:
V=−4GmA
- The magnitude of the gravitational field strength at the center is:
E=4GmA2
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.44videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.56videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Exercise 13.29videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Five point masses m each are kept at five vertices of a regular pentagon. Distance of center of pentagon from any one of the vertice is 'a'. Find gravitational potential and filed strength at center.
View SolutionTwo points masses m each are kept at the two verticle of an equilateral triangle of side 'a' as shows in figure.

Find gravitational potential and magnitude of field strength at O.View SolutionThree point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .View Solution
.View SolutionFour point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
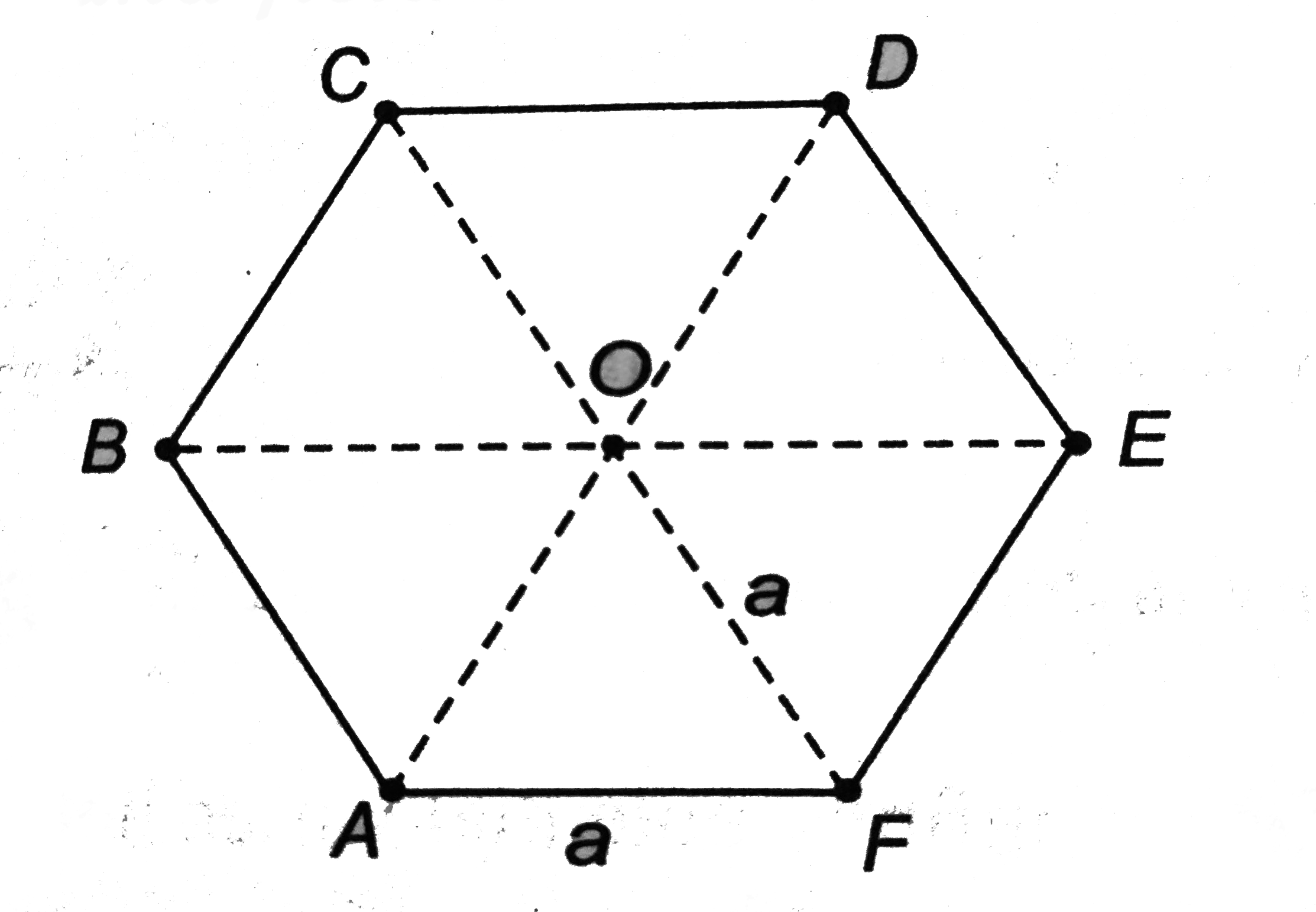 .View Solution
.View SolutionTwo concentric speherical shells are as shown in figure. The magnitude of gravitational potential (V) and field strength (E ) vary with distance ( r) from centre as
 View Solution
View SolutionAssertion : In moving from centre of a solid sphere to its surface, gravitational potential increases.
Reason : Gravitational field strength increase.View SolutionFind the potential V at P in the gravitational field of fixed point mass M.
View SolutionThree mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
View SolutionThree identical point objects each of mass m are placed at the vertices of an equilateral triange of side l. What is the gravitational potential at the centre of the equilateral triangle due to the point masses?
View SolutionTwo concentric shells have masses M and m and their radii are R and r, respectively, where R>r. What is the gravitational potential at their common centre?
View Solution

