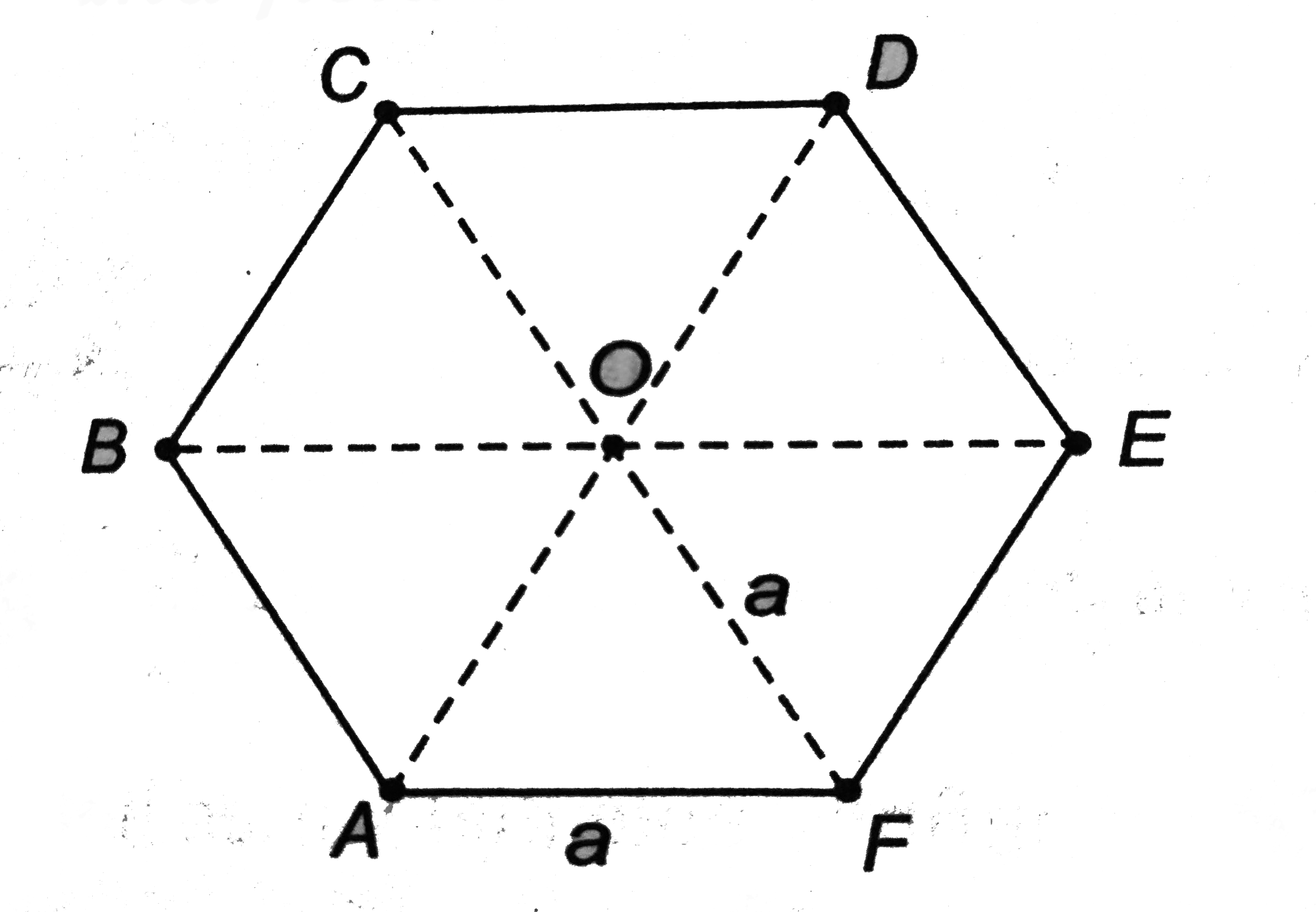
Four point masses easch of mass 'm' are placed at four vertieces A, B, C, nd D of a regular hexagon of side 'a' as shown in figure , Find gravitational potential and field strength at the centre O of the hexagon.
 .
.
−4Gma,√3(Gm)a2
−4Gma,√3(Gm)2(a2)
−Gma,√3(Gm)a2
−2Gma,√3(Gm)a2
The correct Answer is:A, B, C
Gravitational potential id scalar quantity. Therefore,
V0=scalar sul of gravtational potentials produced by four point massses at A, B, C, and D.
=Gma−Gma−Gma
=−4Gma
gravtational field strength is a vector quantity. So, it is a vector sum of four vectors of equal magnitudes.
E=Gma2=EA=EB=FC=ED
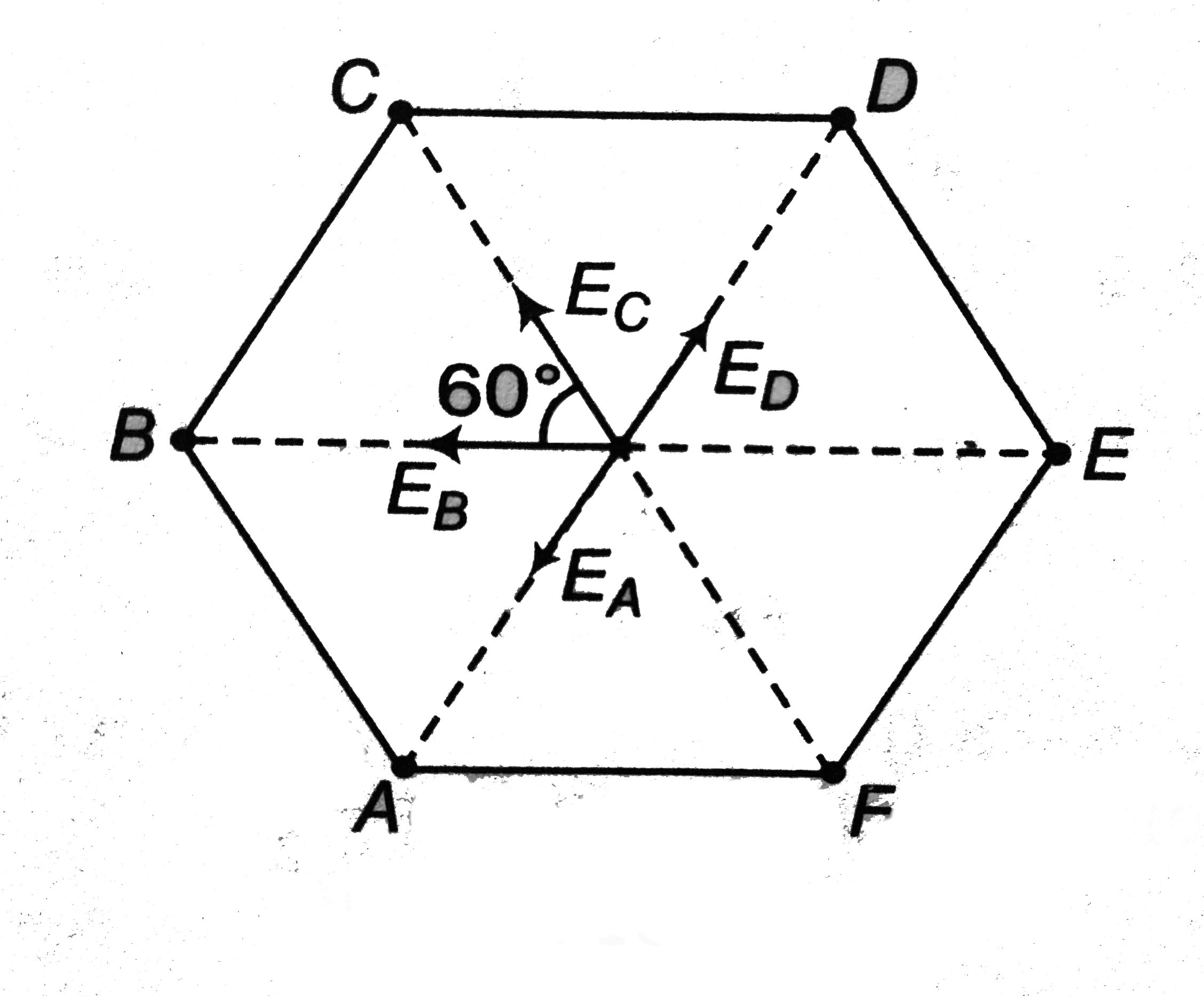
EA and ED are cancelled. So, net field dtrength is a vector sum of EB and EC at angle 60∘.
∴E≠t=√E2+E2+2(E)(E)cos60∘=√3E
=√3(Gm)a2
this net field strength is along the bisector line of ∠COB, away from O, between EC and EB.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Solved Examples16videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Miscellaneous Examples8videos
GRAVITATION
- BOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE2videos
GENERAL PHYSICS
- BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE10videos
KINEMATICS
Similar Questions
Three point masses 'm' each are kept at three verties of a square pf side 'a' as shown in figure. Find gravitation potential and field strength at point O.
 .View Solution
.View SolutionTwo points masses m each are kept at the two verticle of an equilateral triangle of side 'a' as shows in figure.
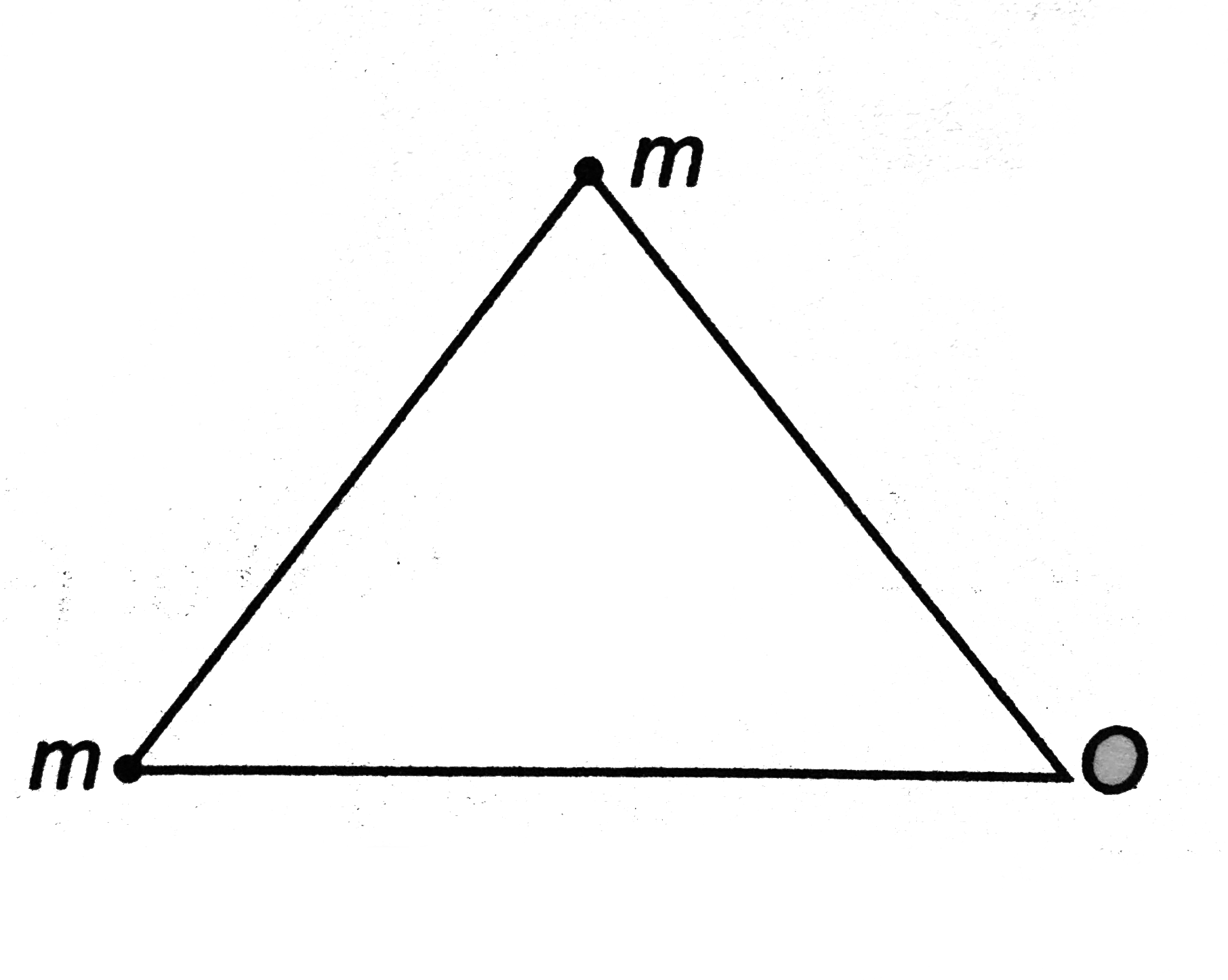
Find gravitational potential and magnitude of field strength at O.View Solution
Knowledge Check
- Question 1 - Select One
Six point charges are arrange at the vertices of a regular hexagon of side length a (shown in figure).
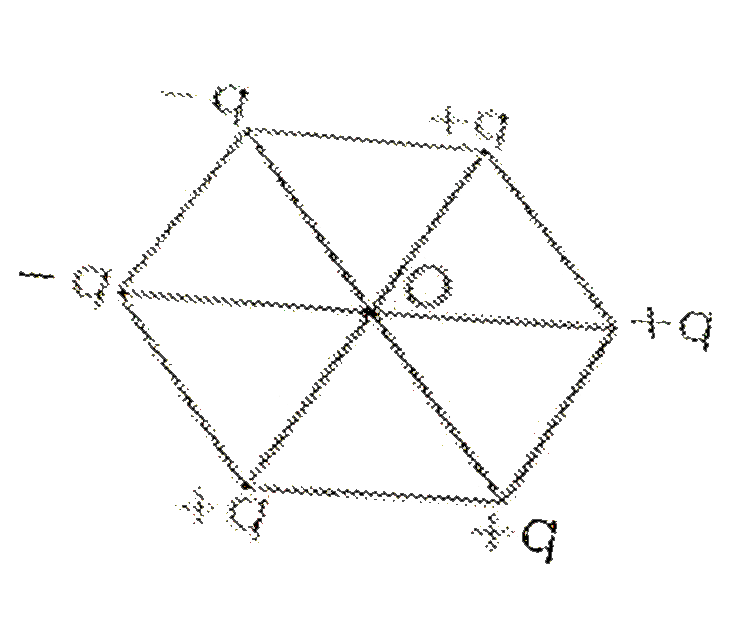
Find the magnitude of electric field at the centre of regular hexagon.A−qB−q6C+1.83qD−1.83q - Question 2 - Select One
Six point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
AGm2l2[54+1√3]BGm2l2[34+1√3]CGm2l2[54−1√3]DGm2l2[34−1√3]
Five point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
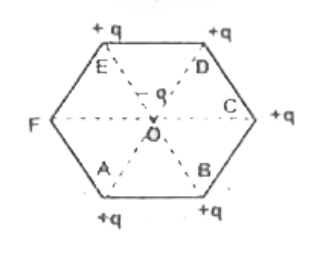 View Solution
View SolutionFour point masses each of mass m are placed on vertices of a regular tetrahedron. Distance between any two masses is r.
View SolutionAssertion : Four point masses each of mass m are placed at points 1, 2, 3 and 6 of a regular hexagon of side a. Then the gravitational field at the centre of hexagon is Gma2
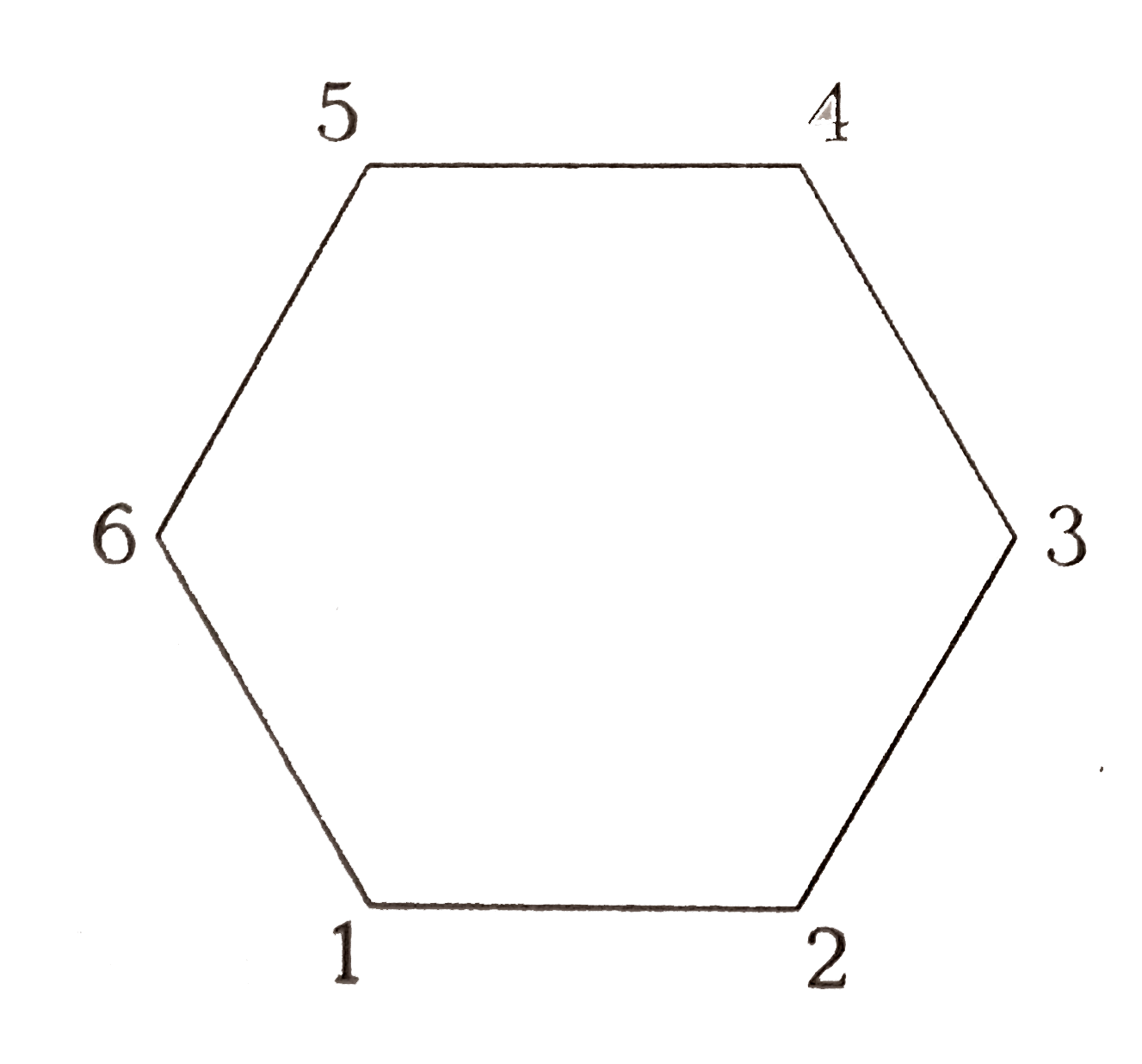
Reason : The field strength due to masses at 3 and 6 are cancelled out.View SolutionFive point masses m each are kept at five vertices of a regular pentagon. Distance of center of pentagon from any one of the vertice is 'a'. Find gravitational potential and filed strength at center.
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionSix particles each of mass 'm' are placed at six verties A,B,C,D,Eand F of a regular hexagon of side 'a'. A seventh particle of mass 'M' is kept at center 'O' of the hexagon.
(a)Find net force on 'M'.
(b)Find net force on 'M' if particles at A is removed.
(c) Find net force on 'M' if particles at A and C are removed .View Solution

