A pendulum has a period T for small oscillations. An obstacle is placed directly beneath the pivot, so that only the lowest one - quarter of the string can follow the pendulum bob when it swings to the left of its resting position. The pendulum is released from rest at a certain point. How long will it take to return to that point again ? In answering this question, you may assume that the angle between the moving string and the vertical stays small throughout the motion.

The correct Answer is:B
Half the oscillation is completed with length l and rest half with length l4.
T=T12+T22=12⎡⎣2π√lg+2π
⎷l4g⎤⎦
=34[2π√lg]=34T, where T=2π√lg
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 7
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 8
1 Video
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 5
7 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEY ENGLISHCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
A pendulum has time period T for small oscillations. An obstacle P is situated below the point of suspension O at a distance 3l4. The pendulum is released from rest. Throughout the motion, the moving string makes small angle with vertical. Time after which the pendulum returns back to its initial position is
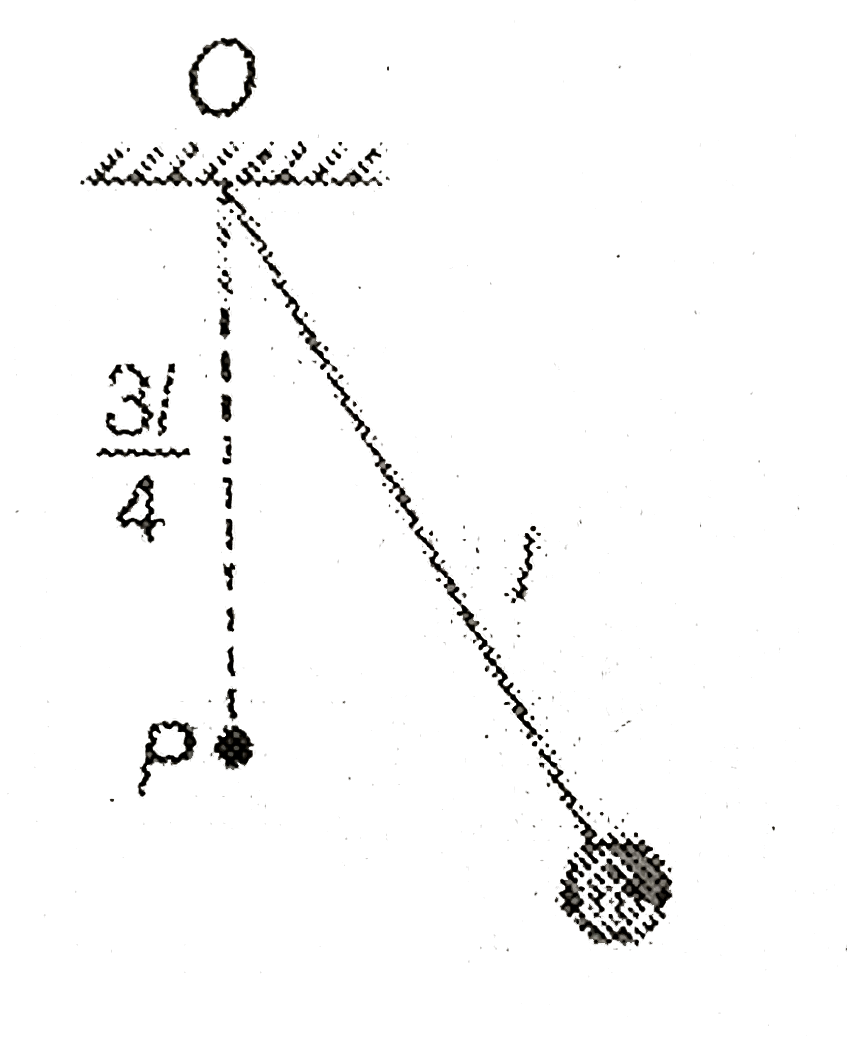
View SolutionA simple pendulum consisting of a mass M attached to a string of length L is released from rest at an angle α. A pin is located at a distance l below the pivot point. When the pendulum swings down, the string hits the pin as shown in figure. The maximum angle θ which the string makes with the vertical after hitting the pin is

View Solution
Knowledge Check
A pendulum is oscillaring on either side its rest position.The correct statement is:
AIt has the maximum potential energy at its extreme position.BIt has the maximum kinetic energy at its extreme position.Cit has the maximum potential energy at its mean position.DThe sum of its kinetic and potential energies remains constant throughout the motion.
It takes 0.2 s for a pendulum bob to move from the mean position to one end. What is the time period of the pendulum?
View SolutionA pendulum is oscillating on either side of its rest position. Explain the energy changes that take place in the Oscillating pendulum. How does mechanical energy remain constant in it ? Draw the necessary diagram.
View SolutionA simple pendulum is released from rest with the string in horizontal position. The vertical component of the velocity of the bob becomes maximum, when the string makes an angle θ with the vertical. The angle θ is equal to
View SolutionA simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
View SolutionWhen the point of suspendion of pendulum is moved, its period of oscillation
View SolutionIn a simple pendulum, the breaking strength of the string is double the weight of the bob. The bob is released from rest when the string is horizontal. The string breaks when it makes an angle θ with the vertical.
View SolutionIn a simple pendulum the period of oscillation (T) is related to the length of the pendulum (L) as
View Solution
