A simple pendulum suspended from the roof off a lift oscillates with frequency υ when the lift is at rest. If the lift falls freely under gravity, its frequency of oscillation becomes
30∘
45∘
60∘
90∘
The correct Answer is:D
At mean position,
mg+mv2r=3mg⇒v=√2gl…..(i)
and if the body displace by angle θ with vertical, then
v=√2gl(1−cosθ)……(ii)
On comparing Eqs. (i) and (ii), we get
cosθ=0⇒θ=90∘
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Match the columns
3 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CIRCULAR MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - CIRCULAR MOTIONEXERCISE - Check point
45 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEY ENGLISHCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEY ENGLISHCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
A simple pendulum completes 40 oscillations in one minute. Find its frequency
View SolutionA simple pendulum is suspended from the ceiling of a car and its period of oscillation is T when the car is at rest. The car starts moving on a horizontal road with a constant acceleration g (equal to the acceleration due to gravity, in magnitude) in the forward direction. To keep the time period same, the length of th pendulum
View Solution
Knowledge Check
A simple pendulum is oscillating in a stationery lift. When the lift falls freely, the frequency of oscillations of the pendulum is
AzeroBυC2υDinfiniteA pendulum suspended from the ceiling of train has a period T When the train is at rest. When the train si accelerating with a uniform acceleratio a, the period of oscillation will
AincreaseBdecreaseCremained unaffectedDbecomes infiniteA simple pendulum is suspended from the ceiling of a stationary elevator and it oscillates with a small amplitude if the elevator accelerates upwards, the
Afrequency of oscillation of pendulum increasesBfrequency of the oscillations of the pendulum decreasesCpendulum stops oscillatingDtime period of oscillations remain same but the amplitude increases
What is the frequency of oscillation of a simple pendulum mounted in a cabin that is freely falling under gravity ?
View SolutionA simple pendulum suspended from the celling of a stationary lift has period T0. When the lift descends at steady speed, the period is T1, and when it descends with constant downward acceleration, the period is T2 which one of the following is true?
View SolutionA simple pendulum is hanging from the roof of a trolley which is moving horizontally with acceleration g. If length of the string is L and mass of the bob is m, then time period of oscillation is
View SolutionA simple pendulum 50cm long is suspended from the roof of a acceleration in the horizontal direction with constant acceleration √3gm/s−1. The period of small oscillations of the pendulum about its equilibrium position is (g=π2m/s2) ltbRgt
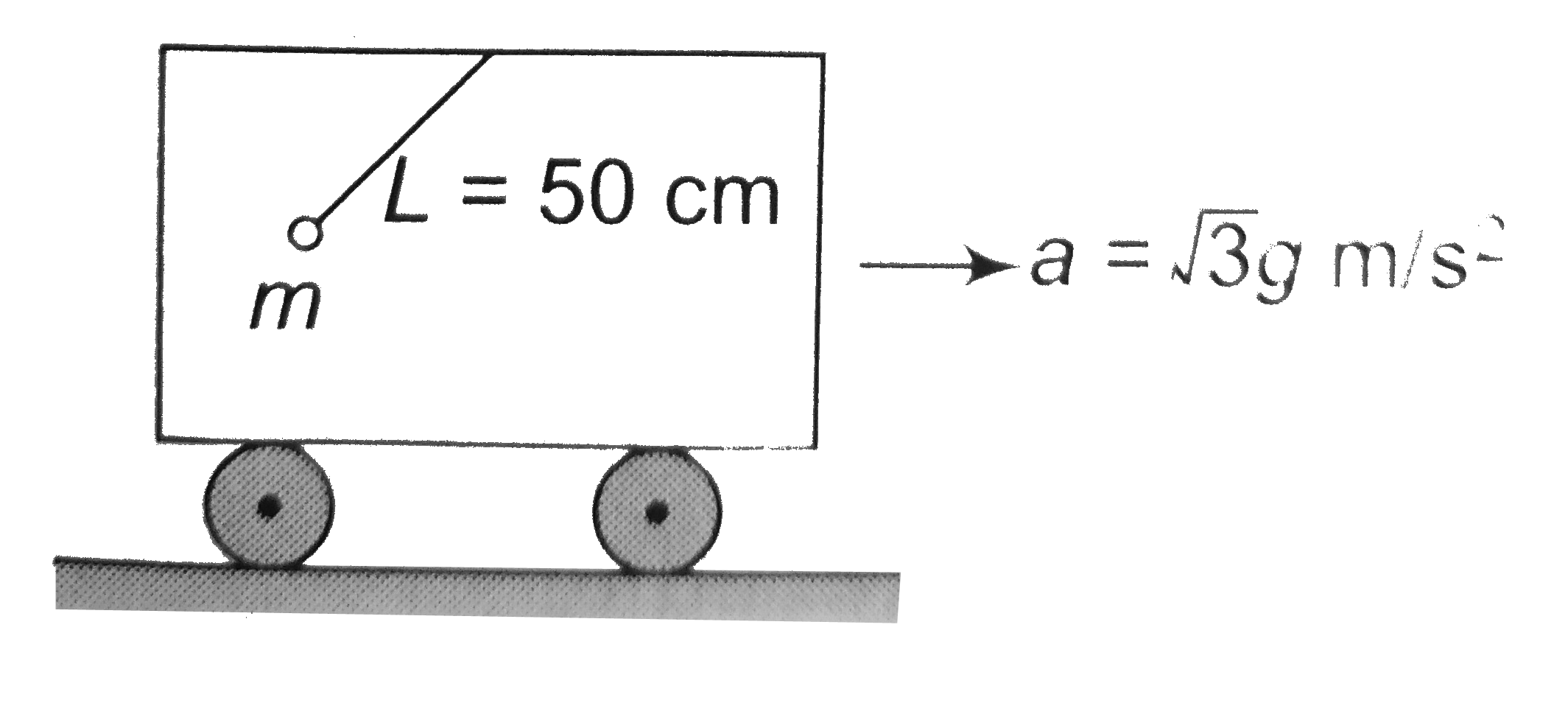
View SolutionA pendulum is suspended in a ligt and its period of oscillation when the lift is stationary is Ta. What must be the accleraion of the lift for the period of oscillation of the pendulum to be T0/2?
View Solution
